2015-06-04
7390
Импульсной характеристикой h(n) линейной дискретной цепи называется ее реакция на дискретную дельта-функцию δ(n) при нулевых начальных условиях.
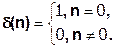(1.6)
Признаком нулевых начальных условий является отсутствие реакции при отсутствии воздействия.
Важно помнить, что:
- как и разностное уравнение, импульсная характеристика описывает дискретную цепь во временной области;
- определить импульсную характеристику дискретной системы можно двумя способами:
1. по разностному уравнению, решая его методом прямой подстановки;
2. по передаточной функции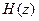 
путем деления полинома числителя на знаменатель
- импульсная характеристика нерекурсивной цепи имеет конечную длительность, значения отсчетов равны коэффициентам разностного уравнения;
- импульсная характеристика рекурсивной цепи имеет бесконечную длительность;
- для достижения необходимой точности при вычислении импульсной характеристики надо учесть все отсчеты, значения которых превышают 10% от максимального значения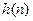 
.
1 способ: (для четных вариантов)
Допустим, что на вход дискретной цепи действует дельта-функция вида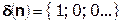 
. Тогда, согласно разностному уравнению цепи:
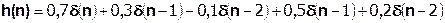(1.7)
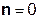
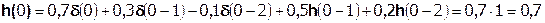
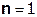
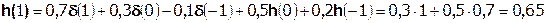
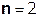
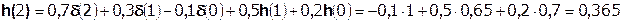
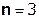
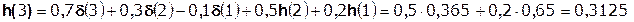
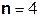
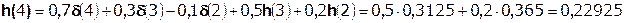
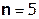
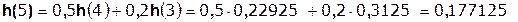
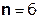
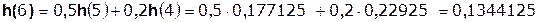
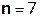
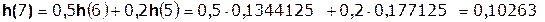
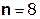
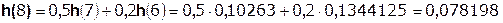
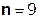
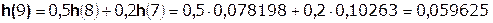
Так как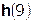 
составляет ≈ 8,5 % от 
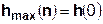, т.е. не превышает 10%, дальнейшие отчеты импульсной характеристики цепи считать не имеет смысла.
2 способ: (для нечетных вариантов)
Импульсную характеристику дискретной цепи можно найти по передаточной функции, выполнив ее обратное z-преобразование. Обратное z-преобразование передаточной функции можно осуществить путем последовательного деления полинома числителя Н(z) на знаменатель с поочередным выделением слагаемых вида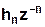 
.
Выполним деление передаточной функции Н(z):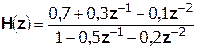 
 |
 |
|
…….
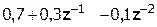
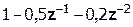
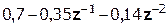
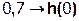
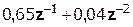
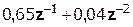
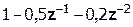
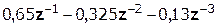
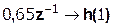
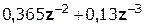
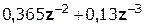
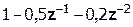
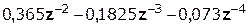
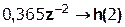
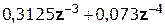
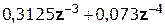
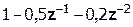
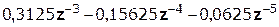
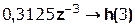
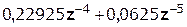
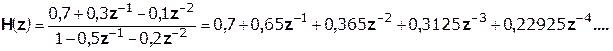
Деление осуществляем до тех пор, пока не достигнем 10% от hmax(n).
Таблица 1.1 Импульсная характеристика дискретной цепи
| n | h(n) |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 | |
 |
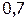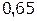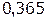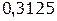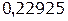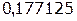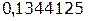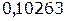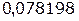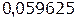Построим график импульсной характеристики цепи:
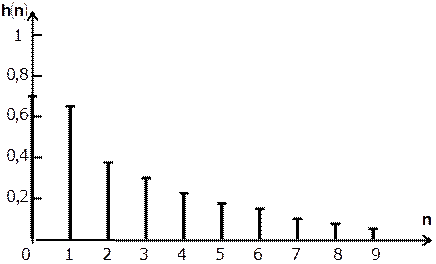
Рисунок 1.2 - Импульсная характеристика цепи
