2015-06-04
3300
Частотная характеристика линейной дискретной цепи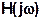 
- фурье-изображение импульсной характеристики 
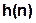. Также выражение 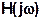можно получить из передаточной функции цепи 
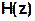, выполнив замену 
.
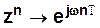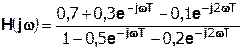(1.8)
Как и всякую комплексную функцию, 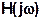можно представить через модуль и аргумент
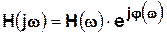, (1.9)
где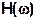 
- амплитудно-частотная характеристика (АЧХ) цепи,
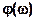- фазо-частотная характеристика (ФЧХ) цепи.
Для определения частотных характеристик цепи и сигнала часто применяют нормирование по частоте: 
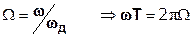(1.10)
Запишем передаточную функцию исходной цепи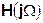 
. Согласно выражению (1.8), получим:
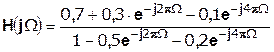(1.11)
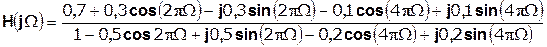(1.12)
Амплитудно-частотная характеристика дискретной цепи:
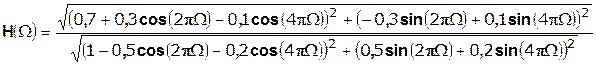(1.13)
Фазо-частотная характеристика дискретной цепи:
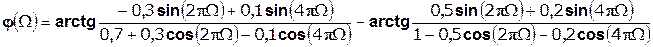
(1.14)
При расчетах важно помнить, что:
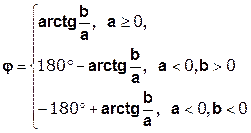
Расчеты удобно свести в таблицу:
Таблица 1.2 – Частотные характеристики цепи
| Ω | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | ||
| H(Ω) | 1,27 | 0,77 | 0,56 | 0,375 | 0,231 | 0,375 | 0,56 | 0,77 | 1,27 | ||
| φ(Ω) | -47,3 | -45,1 | -41,8 | -36,9 | 36,9 | 41,8 | 45,1 | 47,3 |
Так как частотные характеристики дискретных цепей (сигналов) являются непрерывными периодически повторяющимися функциями, достаточно построить частотные характеристики только для одного периода, соответствующего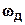 
.
тогда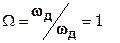 
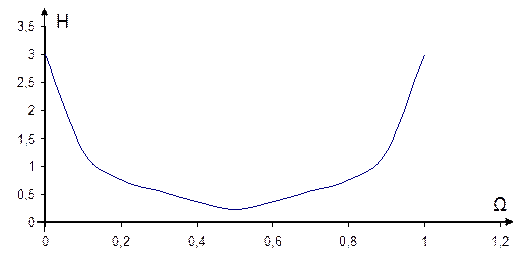
Рисунок 1.3 - АЧХ дискретной цепи
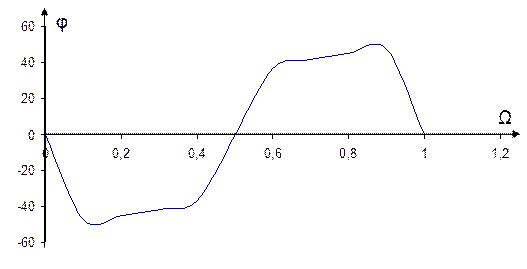
Рисунок 1.4 – ФЧХ дискретной цепи
Как видно из рисунков 1.3 и 1.4 АЧХ является непрерывной периодически повторяющейся четной функцией, а ФЧХ – непрерывной периодически повторяющейся нечетной функцией.
