Предполагается, что значение 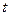 и значение функции в начале и в конце интервала интегрирования нефиксированные. Может быть также частный случай, когда подвижна одна граница (верхняя или нижняя), когда нижняя или верхняя границы задаются в виде кривой или поверхности, т.е. задается функционально. Рассмотрим случай, когда варьируется верхняя граница, тогда
и значение функции в начале и в конце интервала интегрирования нефиксированные. Может быть также частный случай, когда подвижна одна граница (верхняя или нижняя), когда нижняя или верхняя границы задаются в виде кривой или поверхности, т.е. задается функционально. Рассмотрим случай, когда варьируется верхняя граница, тогда
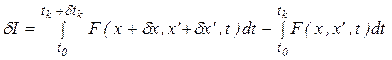 ;
;
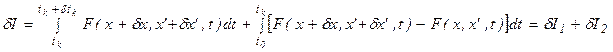 ;
;
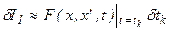 ;
;
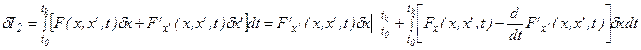
Если функция 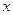 является экстремалью, то подынтегральное выражение должно быть равно нулю в соответствии с уравнением Эйлера:
является экстремалью, то подынтегральное выражение должно быть равно нулю в соответствии с уравнением Эйлера: 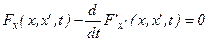 .
.
Т.к. значение функции не фиксировано в точке 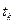 , то
, то 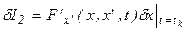 , тогда
, тогда 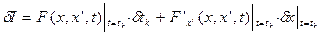 .
.
Поскольку варьируется и 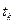 и значение функции в точке
и значение функции в точке 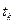 , то полная вариация
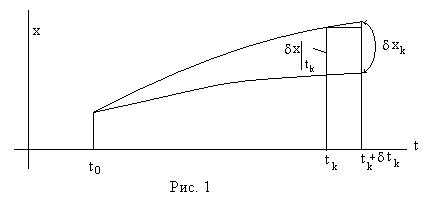
, то полная вариация 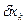 может быть представлена (см рис. 1):
может быть представлена (см рис. 1): 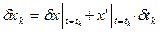 ;
;
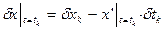
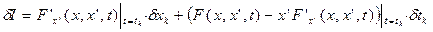 (*)
(*)
Для обеспечения экстремума вариация функционала должна быть равна нулю: 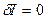 , тогда, при независимых
, тогда, при независимых 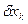 и
и 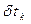 вариация будет равна нулю, если
вариация будет равна нулю, если 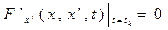 и
и
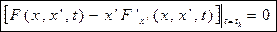
Эти уравнения используются для нахождения 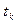 и второй константы интегрирования, они называются условиями трансверсальности.
и второй константы интегрирования, они называются условиями трансверсальности.
Если вариации 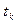 и
и 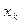 связаны зависимостью
связаны зависимостью 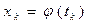 , т.е. верхний конец интервала перемещается по некоторой кривой, тогда
, т.е. верхний конец интервала перемещается по некоторой кривой, тогда 
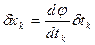 , и условия трансверсальности записываются следующим образом:
, и условия трансверсальности записываются следующим образом:
1) 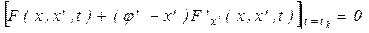
(получено путем подстановки 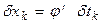 в формулу (*), приравнивания вариации к нулю и деления на
в формулу (*), приравнивания вариации к нулю и деления на 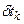 ).
).
Аналогично записывается уравнение трансверсальности для нижней границы, если
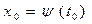
2) 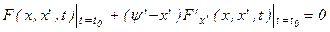 .
.
 2015-06-05
2015-06-05 691
691








