Рассмотрим функционал в виде интеграла от функции 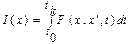 , где
, где
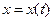 ,
, 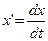 ,
, 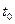 и
и 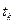 - фиксированные.
- фиксированные.
Найти функцию 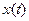 , обеспечивающую экстремум функционала и удовлетворяющую граничным условиям:
, обеспечивающую экстремум функционала и удовлетворяющую граничным условиям: 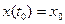 ,
, 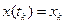 .
.
Определим приращение функционала как 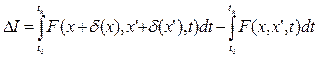 , причем, функция
, причем, функция 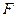 дифференцируема по
дифференцируема по 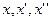 , а
, а
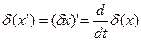 ;
;
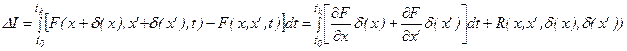
Для малых вариаций функции и ее производной (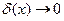 ,
, 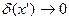 )
)
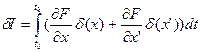 .
.
Интегрируем второе слагаемое по частям:
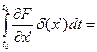
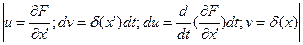
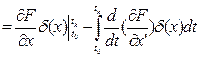 .
.
Поскольку в точках 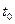 и
и 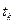 функция
функция 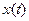 задана своими граничными значениями (она не изменяется в этих точках), вариации функции в них равны нулю и первое слагаемое также будет равно нулю. Тогда вариация функционала
задана своими граничными значениями (она не изменяется в этих точках), вариации функции в них равны нулю и первое слагаемое также будет равно нулю. Тогда вариация функционала 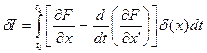 .
.
Чтобы обеспечить экстремум функционала, функция 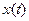 должна быть такой, чтобы вариация
должна быть такой, чтобы вариация 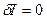 .
.
Лемма: если интеграл 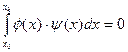 и функция
и функция 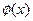 в общем случае не равна нулю на интервале
в общем случае не равна нулю на интервале 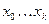 , неравенство будет выполняться, если
, неравенство будет выполняться, если 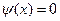 .
.
Применительно к вариации функционала при произвольно изменяющемся 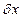 ,
, 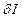 будет равно нулю, если выражение
будет равно нулю, если выражение 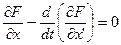 .
.
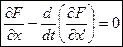 - уравнение Эйлера
- уравнение Эйлера
Решением приведенного уравнения Эйлера является функция 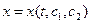 , зависящая от двух констант, поскольку это дифференциальное уравнение второго порядка. Она доставляет экстремум исходному функционалу и называется экстремалью. Константы
, зависящая от двух констант, поскольку это дифференциальное уравнение второго порядка. Она доставляет экстремум исходному функционалу и называется экстремалью. Константы 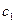 и
и 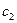 определяются из граничных условий
определяются из граничных условий 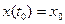 ,
, 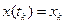 .
.
Уравнение Эйлера можно расписать как: 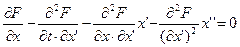 т. к.
т. к.
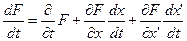
Уравнение Эйлера для функции, зависящей от множества переменных:
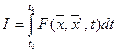 ;
;
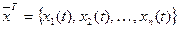 ;
;
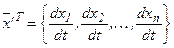 .
.
Поскольку 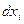 не зависят друг от друга, вариация функционала будет равна сумме частных производных, умноженных на вариации собственно функций и их производных, и уравнение Эйлера переходит в систему уравнений:
не зависят друг от друга, вариация функционала будет равна сумме частных производных, умноженных на вариации собственно функций и их производных, и уравнение Эйлера переходит в систему уравнений: 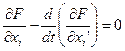 ,
, 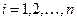 .
.
 2015-06-05
2015-06-05 314
314








