Найти экстремаль, обеспечивающую экстремум функционала: 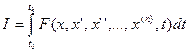
при следующих граничных условиях:
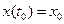 ,
, 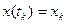 ,
,
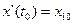 ,
, 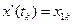 ,
,
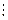
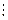
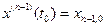
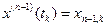 .
.
Решить эту задачу можно:
- путем ввода новых переменных: 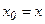 ,
, 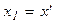 ,
, 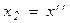 ,..., что позволит записать систему уравнений Эйлера, решая которую находим промежуточные переменные и искомое
,..., что позволит записать систему уравнений Эйлера, решая которую находим промежуточные переменные и искомое 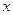 ;
;
- можно воспользоваться уравнением Эйлера-Пуассона, вывод которого дан ниже.
Вариация функционала в данном случае равна
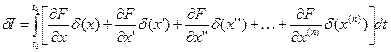 .
.
Интеграл первых двух слагаемых рассматривался выше, а интеграл для третьего слагаемого:
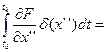
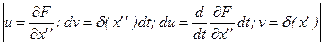
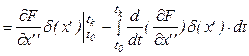 .
.
Первое слагаемое последнего выражения равно нулю, т.к. 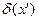 в точках
в точках 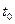 и
и 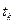 равно нулю. Второе слагаемое снова интегрируем по частям:
равно нулю. Второе слагаемое снова интегрируем по частям: 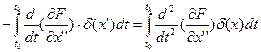 .
.
Интегрируя по частям остальные слагаемые в вариации функционала, получим: 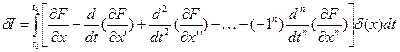 .
.
Аналогично выводу уравнения Эйлера, запишем уравнение Эйлера-Пуассона:
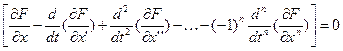
 2015-06-05
2015-06-05 1801
1801








