Проверка экстремума

Если на плоскости 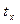через каждую точку некоторой области 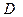проходит только одна кривая семейства 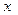, , 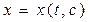то семейство кривых в области 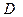образует собственное поле. Угловой коэффициент наклона касательной 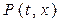к кривой семейства 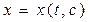, проходящей через точку 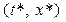называется наклоном поля в точке .

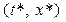Если кривые в области 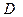пересекаются только в одной точке, то они образуют центральное поле. Если кривые являются экстремалями некоторого функционала, то они образуют поле экстремалей. Для экстремали 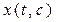, включенной в центральное поле, вариация функционала 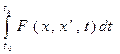может быть записано как:

,

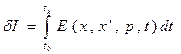где 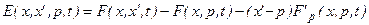- называется функцией Вейерштрассе, 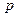- наклон поля на экстремали, т.е. 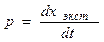. Очевидно, если подинтегральная функция 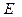будет больше нуля при отклонении функции от экстремали, то функционал на экстремали имеет минимум. Если 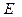меньше нуля – максимум. Причем если 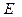сохранят знак при любых отклонениях 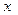от экстремали, то экстремум называют сильным. Если же знак сохраняется только при малых отклонениях 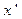от 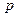, экстремум – слабый. Разложим функцию 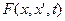по переменной 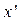в окрестности точки 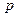в ряд Тейлора: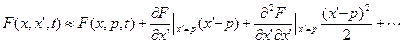

Ограничимся первыми тремя членами ряда и сопоставим полученное выражение с функцией Вейерштрассе (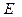). Перенесем первых два слагаемых ряда Тейлора влево, поставив знак точного равенства, тогда в левой части будет функция :

.

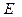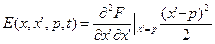Т.к. разность в скобках возводится в квадрат, знак функции 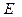определяется второй производной. Т.е. если 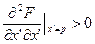, то функционал на экстремали будет иметь минимум. Если 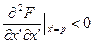, то функционал на экстремали будет иметь максимум. Эти условия называются условиями Лежандра. Если функционал зависит от нескольких функций и их производных, то составляют матрицы и проверяют знаки всех диагональных определителей, если >0 – минимум, <0 – максимум.