2015-06-05
403
Задачи называются задачами на условный экстремум, если имеются ограничения типа «равенство», объединяющие функции, их производные, причем, такие задачи называются задачами классического вариационного исчисления. Задачи с ограничениями в виде неравенств относятся к неклассическому вариационному исчислению.
Для функционала вида: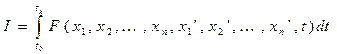 
при наличии ограничений 
, 
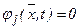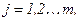
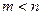в виде алгебраических уравнений, также как и в задачах нелинейного программирования записывают функцию Лагранжа 
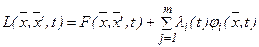с неопределенными множителями 
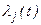. А систему уравнений Эйлера записывают для функции Лагранжа: 
, 
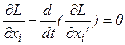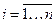. Совместно с уравнениями ограничений 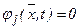, система уравнений Эйлера – Лагранжа позволяет найти 
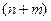неизвестных функци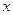й 
и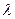 
(примем без доказательств).
Аналогично определяются экстремали, если уравнение связи представлены дифференциальными уравнениями первого порядка: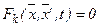 
, k=1,2,...
Если уравнения ограничений записаны в интегральной форме (изопериметрические ограничения)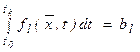 
, 
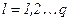, то введение дополнительной переменной 
, 
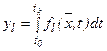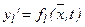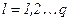, позволяет привести эти уравнения к дифференциальным с добавлением q- новых функций, причем, добавляются граничные условия:
, 
.
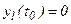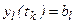Функция Лагранжа будет иметь вид: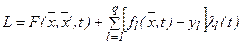 
,
система уравнений Эйлера - Лагранжа
, ;
, 
.
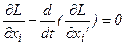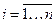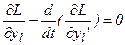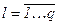Из последней системы получаем систему:
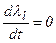и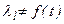 
.
Следовательно, при наличии изопериметрических ограничений в функцию Лагранжа включаются подынтегральные выражения, умноженные на коэффициенты Лагранжа.
