Если функционал представлен интегралом и неинтегральной составляющей, то задача - смешанная.
Для функционала 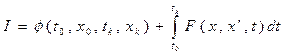 найти экстремаль, если граничные условия заданы в виде:
найти экстремаль, если граничные условия заданы в виде: 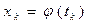 ,
, 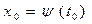 , т.е. не закреплены. Для случая, когда границы закреплены, функция
, т.е. не закреплены. Для случая, когда границы закреплены, функция 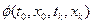 является константой и ее добавление к интегральной части не изменит положение экстремума.
является константой и ее добавление к интегральной части не изменит положение экстремума.
Если граничные точки не закреплены, то вариация функционала рассматривается для случая, когда 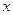 выбирается из пучка экстремалей (является экстремалью для функционала). Такая вариация будет записываться:
выбирается из пучка экстремалей (является экстремалью для функционала). Такая вариация будет записываться: 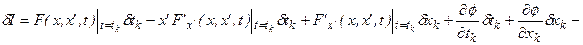
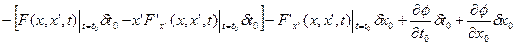 .
.
Аналогично рассмотренному ранее 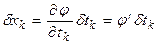 ,
,
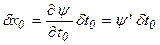 .
.
Приравнивая 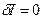 и учитывая, что
и учитывая, что 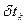 и
и 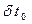 независимые, запишем условие трансверсальности для смешанной задачи:
независимые, запишем условие трансверсальности для смешанной задачи:
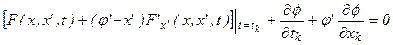
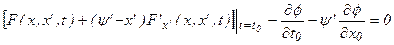
Эти условия дополняют граничные условия и позволяют решить задачу поиска конкретной экстремали, а именно определить константы интегрирования и граничные значения 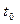 и
и 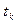 .
.
 2015-06-05
2015-06-05 534
534








