2015-06-05
333
1. 
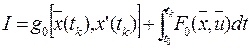
2. 
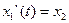
3. 
;
, 
;
, 
;
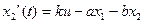
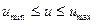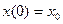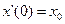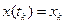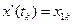- не задано.
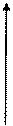
Задачу будем решать на фазовой плоскости с равномерной сеткой, начиная с конечной точки. i
 |
i,j
пусть будет оптимальное управление
x1,k
 |
х1
Задача численного решения заключается в поиске для каждого узла сетки управляющего воздействия, обеспечивающего перевод в следующий узел по оптимальной траектории в смысле заданного критерия оптимальности.
.
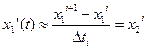Поскольку сетка имеет постоянный шаг:
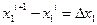- шаг.
;
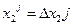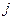- количество шагов по 
.
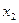Для перехода из одного узла сетки в другой, отстоящий от предыдущего на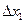 
, требуется различное время 
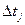, которое определяется фактически величиной 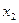той точки, из которой осуществляется переход.
4. 
,
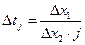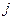- можно считать номером узла, отсчитываемом от оси абсцисс вертикали.
Из (3):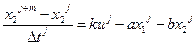 
Для перехода между узлами соседнего по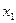 
- сечению, но отличаться по 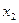на величину 
, (
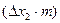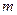может быть положительной и отрицательной целочисленной) требуется одно и тоже время 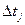, но различается управление.
5. 
/ 
;
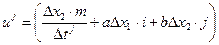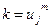Минимальное значение критерия
6. 
;
.
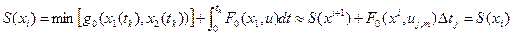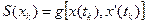Алгоритм расчета оптимального управления:
1. Для конечной точки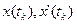 
находим значение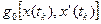 
2. Для узлов предпоследнего сечения по 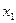находим управляющее воздействие по 
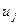, необходимое для перевода из узлов с ординатой 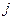предпоследнего сечения в конечную точку. Сравниваем с допустимыми пределами и запоминаем только значения, удовлетворяющими ограничениям по 
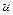. Для каждого узла, из которого возможен переход в конечную точку, определяем значение критерия и также запоминаем.
3. Для всех точек следующего сечения определяем управление, необходимое для перевода в точку предпоследнего сечения и удовлетворяющее ограничениям на управление. Определяем значение критерия и выбираем только тот, который имеет минимальную величину, заполняем это значение и запоминаем соответствующее ему управляющее воздействие. И так до последнего для всех узлов сетки.
4. Формирование управляющего воздействия осуществляется начиная с узла, определенного начальным состоянием системы, по оптимальному управлению для начального узла и так до конечного.
