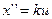 ,
, 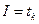 ;
;
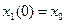 ,
, 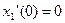 ;
;
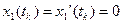 ;
;
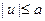 ;
;
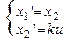 ;
;
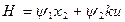 ;
;
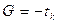 .
.
В соответствии с принципом максимума Понтрягина управляющее воздействие 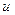 должно обеспечить в явном виде в каждый момент времени
должно обеспечить в явном виде в каждый момент времени 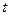 максимум функции Гамильтона.
максимум функции Гамильтона.
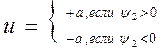 .
.
Разделив второе уравнение системы на первое:
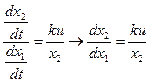 ;
;
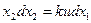 .
.
Поскольку 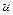 постоянное на интервале, то для интервала постоянства
постоянное на интервале, то для интервала постоянства 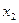 будет иметь вид:
будет иметь вид:
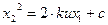 ;
;
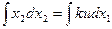 .
.
Фазовый портрет будет иметь вид:
х2
 |
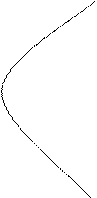

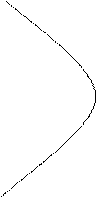
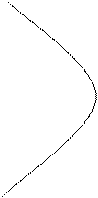
 u=-a u=+a
u=-a u=+a
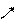 | |||||||
 | |||||||
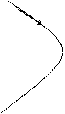 | |||||||
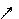 | |||||||

 с0 с2 х1
с0 с2 х1
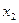 - скорость.
- скорость.
Задача системы управления заключается в переводе системы из некоторого начального состояния 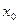 в начало координат (для этой задачи) за минимальное время. Причем в соответствии с теоремой о переключениях количество переключений не будет равно единице. Таким образом в соответствии с фазовым портретом устройство управления должно выбрать начальное управляющее воздействие (
в начало координат (для этой задачи) за минимальное время. Причем в соответствии с теоремой о переключениях количество переключений не будет равно единице. Таким образом в соответствии с фазовым портретом устройство управления должно выбрать начальное управляющее воздействие (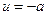 ), которое заставит объект двигаться по фазовой траектории приближаться по
), которое заставит объект двигаться по фазовой траектории приближаться по 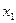 к началу координат. При пересечении с фазовой траекторией, проходящей через начало координат, нужно переключать воздействие на противоположное (
к началу координат. При пересечении с фазовой траекторией, проходящей через начало координат, нужно переключать воздействие на противоположное (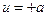 ), чтобы координаты объекта изменялись по траектории, проходящей через начало координат. Участки фазовых траекторий, проходящие через конечную точку и направление в этой конечной точке называется линиями переключения. Для линии переключения, проходящей через начало координат:
), чтобы координаты объекта изменялись по траектории, проходящей через начало координат. Участки фазовых траекторий, проходящие через конечную точку и направление в этой конечной точке называется линиями переключения. Для линии переключения, проходящей через начало координат:
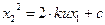 ;
;
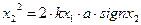 , т.е. знак управления необходимо выбирать.
, т.е. знак управления необходимо выбирать.
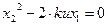 ;
;
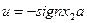 .
.
Нужно выбирать знак 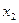 , чтобы скорость стремилась к нулю. Выбор знака управления производится следующим образом: если (1), определяемый текущими координатами находится слева от линии переключения, то управление надо брать положительным, если справа, то отрицательным.
, чтобы скорость стремилась к нулю. Выбор знака управления производится следующим образом: если (1), определяемый текущими координатами находится слева от линии переключения, то управление надо брать положительным, если справа, то отрицательным.
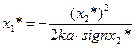 ;
;
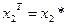 ;
;
 2015-06-05
2015-06-05 399
399







