Синтез замкнутой системы при квадратичном критерии

Рассмотрим на примере. Более общие подходы будут изучены в курсе «Оптимального управления». Для объекта управления 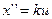найти оптимальное управление для критерия .

, ;

;

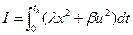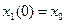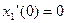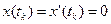Сводим к системе Коши:

;

;

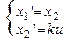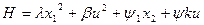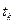- не задано.

Продифференцируем второе уравнение по 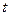и сопоставим с первым.

.

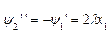Из третьего уравнения:

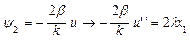, дифференцируем дважды исходное состояние объекта: ;

;

;

.

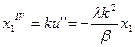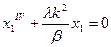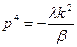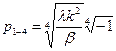По формуле Муавра:

, ;

;

: ;

: ;

: ;

: .

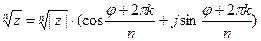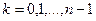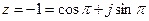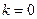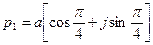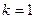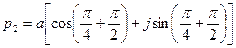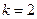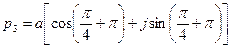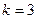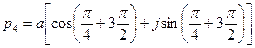Для устойчивости замкнутой системы необходимо, чтобы корни характеристического уравнения были левыми, т.е. с отрицательными действительными частями.

Поскольку часть корней, а именно 1 и 4 будут правыми, т.е. 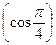и 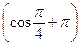будут больше нуля, необходимо, чтобы общее решение ;

.

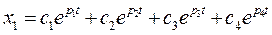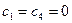Выполнение начальных услови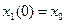й и 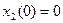достигается за счет констант 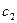и 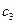. Конечное условие достигается при 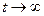, т.к. действительные части корне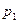й и 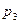отрицательные.

Управляющее воздействие:

1.

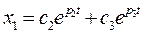
2.

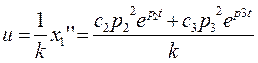
В общем случае получить такое управляющее воздействие можно через функцию:

3.

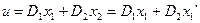
Коэффициенты 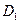и 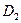можно получить, подставив в (3) 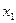из выражения (1) и приравнять полученный результат к (2).

.

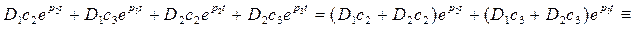
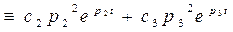Из равенства коэффициентов при экспонентах:

.

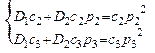Находим 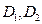. Из условия 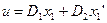синтезируем систему.