Методом динамического программирования.
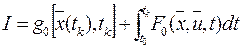 ,
,
объект описывается системой ДУ в форме Коши:
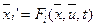 ,
, 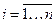 .
.
Требуется определить оптимальное управление 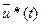 ,
, 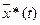 , обеспечивающее минимум критериев и удовлетворяющих уравнениям ограничений:
, обеспечивающее минимум критериев и удовлетворяющих уравнениям ограничений: 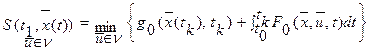 .
.
Сумма первого и последнего слагаемого при оптимальном управлении является функцией Беллмана для начального времени 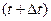 , а интеграл от
, а интеграл от 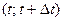 при
при 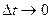 можно заменить приблизительно на производные:
можно заменить приблизительно на производные: 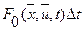 .
.
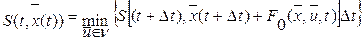 .
.
Поскольку 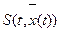 не зависит от
не зависит от 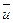 , то эту функцию можно вынести под знак минимума:
, то эту функцию можно вынести под знак минимума:
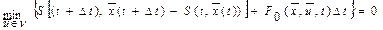 .
.
Разделив все слагаемые на 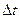 и переходя к пределу при
и переходя к пределу при 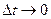 получим:
получим: 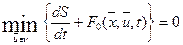 ;
;
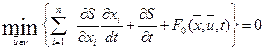 ;
;
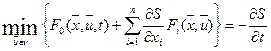 .
.
 2015-06-05
2015-06-05 269
269








