2015-06-05
453
Если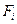 
в явно виде не зависит от 
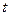, то и функция Беллмана явно не зависит от 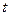. Тогда 
.
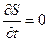Поэтому алгоритм решения задачи:
1. Составляем уравнение Беллмана, формально записывая функцию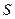 
.
2. Находим оптимальное управление, зависящее от .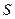
3. Подставляем выражение для оптимального управления в уравнение Беллмана, решаем его и находит функцию .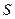
4. Найденные выражения для 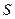подставляем в формулу оптимального управления.
Рассмотрим на примере:
;
;
, 
;
;
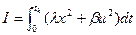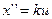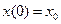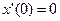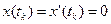Найт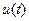и 
и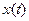 
.
Сводим к системе Коши:
;
;
, 
;
.
-
;
.
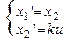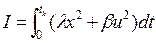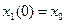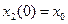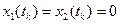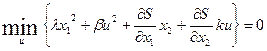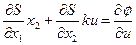- Найдем управление, обеспечивающий экстремум:
;
;
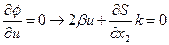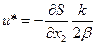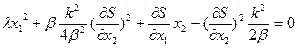
Нелинейное уравнение в частных производных с неизвестной функцией .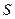
Решение ищем в виде: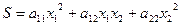 
,
, 
, 
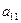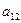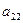- неизвестные коэффициенты.
Подставим решение в уравнение Беллмана и группируем по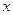 
:
;
.
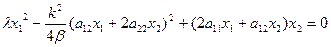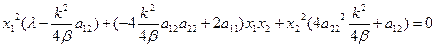Левая часть будет равна нулю, когда коэффициенты при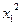 
, 
, 
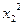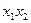будут нулевыми.
;
;
.
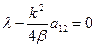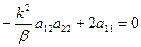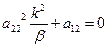Выбираем только квадратичные решения, т.к. квадратичные решения соответствующие минимальной целевой функции должны быть заведомо положительными.
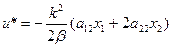- отрицательная обратная связь.
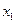- координата, 
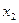- производная.
Управляющее воздействие:
;
, 
.
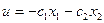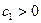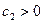Управление является функцией координат объекта и позволяет достаточно просто синтезировать замкнутую систему:
;
.
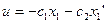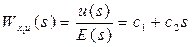E U
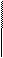
C1 + C2 (s) W0 (s) x1
-
 | |||
 |
Возможность достаточно простого получения передаточных функций замкнутой системы является одним из основных достоинств.
Чтобы получить зависимость от времени координат объекта и управляющего воздействия необходимо подставить в выражение для управления ДУ объекта.
;
.
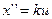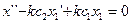Решая это однородное уравнение получаем:
;
, 
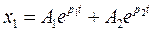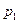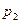- корни характеристического уравнения;
, 
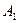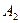- константы интегрирования, полученные из начальных условий. Поскольку 
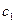и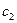 
- положительные, корни характеристического уравнения получаются либо отрицательные действительные, либо с действительными отрицательными частями. Т.е. решение уравнения устойчивое, и 
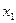сходится к нулю при 
.
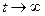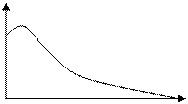
x1
t
Подставляя 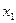и 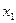, находим зависимость управления от времени. При решении задач оптимального управления методами динамического программирования одной из основных проблем является поиск решения нелинейного ДУ в частных производных.
