Оптимальное поведение обладает тем свойством, что каковы бы не были начальные состояния и решения в начальным момент времени, последующие решения должны составлять оптимальное поведение относительно состояния, получающегося в результате первого решения.
Для динамических систем, описываемых дифференциальными уравнениями, состояние характеризуется набором значений координат в каждый момент времени 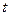 и поведение такой системы определяется изменением координат во времени. Решением является управляющее воздействие на систему (приложенное к системе).
и поведение такой системы определяется изменением координат во времени. Решением является управляющее воздействие на систему (приложенное к системе).
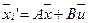 ,
,
есть критерий оптимальности 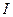 , граничные условия:
, граничные условия:
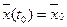 ;
;
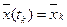 .
.
Если в начальный момент 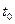 будет определено оптимальное управление и оптимальная траектория
будет определено оптимальное управление и оптимальная траектория 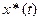 ,
, 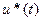 в соответствии с которыми изменяется состояние системы, то система удовлетворяет принципу оптимальности Беллмана, если для любого момента
в соответствии с которыми изменяется состояние системы, то система удовлетворяет принципу оптимальности Беллмана, если для любого момента 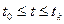 , считать за начальный, будет определено вновь оптимальное управление и траектория и они будут налагаться на первоначально определенное управление и траекторию (совпадут).
, считать за начальный, будет определено вновь оптимальное управление и траектория и они будут налагаться на первоначально определенное управление и траекторию (совпадут).
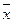


 E
E

 D
D

 B
B
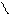
С
 A
A
 t
t
Предположим, что оптимальная траектория 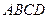 , определенная в начальный момент времени. Пусть с момента
, определенная в начальный момент времени. Пусть с момента 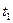 вновь получается оптимальная траектория:
вновь получается оптимальная траектория: 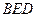 . Если критерий имеет вид:
. Если критерий имеет вид:
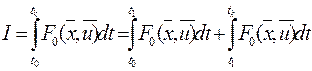
Если 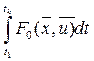 в результате повторного определения и движения по траектории
в результате повторного определения и движения по траектории 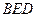 оказался меньше интеграла, первоначально полученного для движения по траектории
оказался меньше интеграла, первоначально полученного для движения по траектории 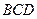 , следовательно, либо первоначальная траектория не была оптимальной, т.к. интеграл может быть еще меньше, либо траектории должны совпадать. При интегральных критериях система управления удовлетворяет принципу оптимальности Беллмана.
, следовательно, либо первоначальная траектория не была оптимальной, т.к. интеграл может быть еще меньше, либо траектории должны совпадать. При интегральных критериях система управления удовлетворяет принципу оптимальности Беллмана.
 2015-06-05
2015-06-05 614
614








