Математический маятник

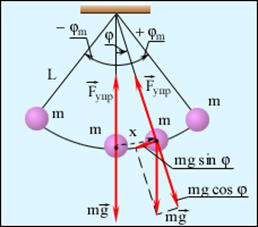
Рис. 54. Математический маятник. φ – угловое отклонение маятника от положения равновесия, x = l φ – смещение маятника по дуге.

Это точка массой m, подвешенная на невесомой нити, и колеблющейся под действием силы тяжести. Момент инерции J = ml², (8.64).

где l - длина маятника. Поскольку математический маятник это частный случай физического маятника, когда вся масса сосредоточена в одной точке, то период его колебаний T = 2pÖl/g. (8.65).

РЕЗОНАНС.

Резкое возрастание амплитуды вынужденных колебаний при сближении частот вынуждающей силы и собственной называется резонансом. При d² << w₀² значение w_рез. практически совпадает с собственной частотой w₀ колебательной систе5ы.

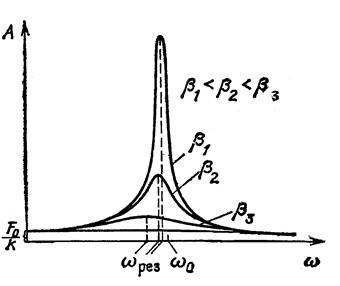
Рис. 55. Набор резонансных кривых.

И получим A_рез. = x₀/2dÖw₀² - d². (8.66).

Амплитуда скорости

wA_рез. = x₀w/Ö(w₀² - w²) +4d²w² = x₀/Ö(w₀² - w²)/w² + 4d². (8.67).

максимальна при w = w₀ и равна x₀/(2d), т.е. чем больше коэффициент затухания d, тем ниже максимум резонансной кривой и амплитуда скорости при резонансе равна A_рез. = x₀/(2d) = F/r. (8.68).

Изображенная на рисунке совокупность графиков функции называется резонансными кривыми. A/x = ω₀/2β = 2π/2βT = π/λ = Q. (8.69).

где 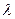-логарифмический декремент затухания. Явления резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различного рода сооружений необходимо, чтобы собственная частота колебаний их не совпадала с частотой возможных внешних воздействий, в противном случае возникнут вибрации, которые могут вызвать серьезные разрушения. С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания, если их частота совпадает с частотой собственных колебаний прибора.