1. 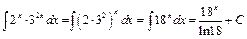 ;
;
2. 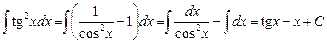 ;
;
3. 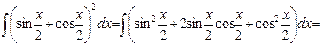
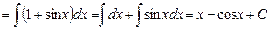 .
.
II. Интегрирование подстановкой (заменой переменной).Пусть требуется вычислить интеграл 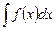 , который не является табличным. Суть метода подстановки состоит в том, что в интеграле
, который не является табличным. Суть метода подстановки состоит в том, что в интеграле 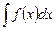 переменную
переменную 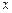 заменяют переменной
заменяют переменной 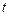 по формуле
по формуле 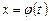 , учитывая
, учитывая 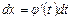 .
.
Теорема 3. Пусть функция 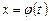 определена и дифференцируема на некотором множестве
определена и дифференцируема на некотором множестве 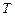 . И пусть
. И пусть 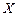 – множество значений функции
– множество значений функции 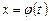 , на котором определена функция
, на котором определена функция 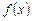 . Тогда если на множестве
. Тогда если на множестве 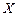 функция
функция 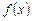 имеет первообразную, то на множестве
имеет первообразную, то на множестве 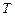 справедлива формула замены переменной
справедлива формула замены переменной
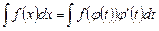 .
.
► Формула справедлива, если после дифференцирования обеих ее частей получаются одинаковые выражения.
Учитывая, что 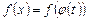 – сложная функция, имеем
– сложная функция, имеем
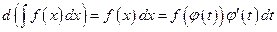 .
.
Продифференцировав правую часть данной формулы, получим
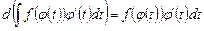 .
.
Таким образом, формула замены переменной в неопределенном интеграле справедлива. ◄
Очень часто при вычислении интегралов пользуются приемом «подведения» подынтегральной функции под знак дифференциала. По определению дифференциала функции имеем 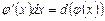 . Переход от левой части этого равенства к правой называют «подведением» множителя
. Переход от левой части этого равенства к правой называют «подведением» множителя 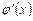 под знак дифференциала.
под знак дифференциала.
Пусть требуется найти интеграл вида
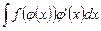 .
.
Внесем в этом интеграле множитель 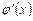 под знак дифференциала, а затем выполним подстановку
под знак дифференциала, а затем выполним подстановку 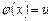
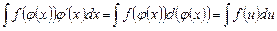 .
.
Если интеграл 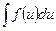 – табличный, его вычисляют непосредственным интегрированием.
– табличный, его вычисляют непосредственным интегрированием.
Пример.
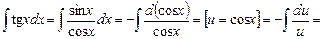
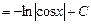 .
.
III. Интегрирование по частям.Метод интегрирования по частям основан на следующей теореме.
Теорема 4. Пусть функции 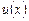 и
и 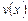 – две дифференцируемые функции переменной
– две дифференцируемые функции переменной 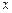 на промежутке
на промежутке 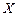 . И пусть функция
. И пусть функция 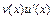 имеет первообразную на этом промежутке, то есть существует интеграл
имеет первообразную на этом промежутке, то есть существует интеграл 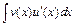 . Тогда функция
. Тогда функция 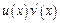 также имеет первообразную, то есть существует интеграл, причем справедлива формула интегрирования по частям:
также имеет первообразную, то есть существует интеграл, причем справедлива формула интегрирования по частям:
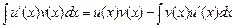 .
.
► Пусть 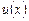 и
и 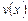 – две дифференцируемые функции переменной
– две дифференцируемые функции переменной 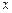 . Тогда
. Тогда
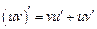 .
.
Отсюда 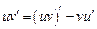 .
.
Интегрируя обе части последнего равенства, получаем
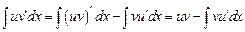 .
.
Интеграл 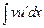 существует по условию, значит существует и интеграл
существует по условию, значит существует и интеграл 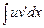 , и имеет место формула
, и имеет место формула 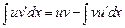 . ◄
. ◄
Замечание. Формулу интегрирования по частям можно записать в виде:
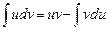 .
.
Формула интегрирования по частям дает возможность свести вычисление интеграла 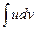 к вычислению интеграла
к вычислению интеграла 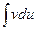 , который может оказаться существенно более простым, чем исходный.
, который может оказаться существенно более простым, чем исходный.
Укажем некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям:
I. Интегралы вида 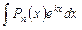 ,
, 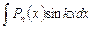 ,
, 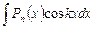 . Здесь
. Здесь 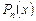 – многочлен степени
– многочлен степени 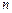 ,
, 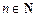 , относительно
, относительно 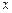 ,
, 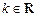 . Чтобы найти эти интегралы, достаточно положить
. Чтобы найти эти интегралы, достаточно положить 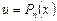 и применить формулу интегрирования по частям
и применить формулу интегрирования по частям 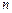 раз.
раз.
II. Интегралы вида 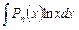 ,
, 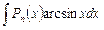 ,
, 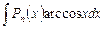 ,
, 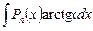 ,
, 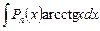 . Здесь
. Здесь 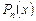 – многочлен степени
– многочлен степени 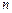 ,
, 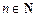 , относительно
, относительно 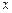 . Данные интегралы вычисляются по частям, принимая за
. Данные интегралы вычисляются по частям, принимая за 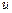 функцию, являющуюся множителем при
функцию, являющуюся множителем при 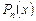 .
.
III. Интегралы вида 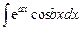 ,
, 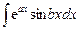 (
(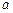 ,
, 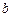 – числа) вычисляются двукратным интегрированием по частям. За
– числа) вычисляются двукратным интегрированием по частям. За 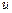 принимают функцию
принимают функцию 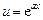 .
.
Примеры.
1. 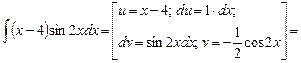
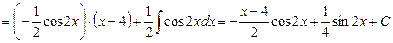 2.
2. 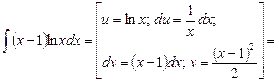
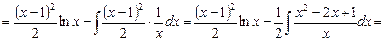
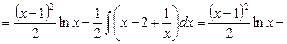
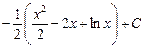 .
.
3. 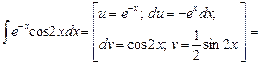
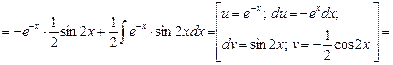
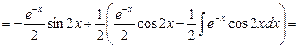
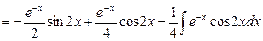 .
.
Отсюда
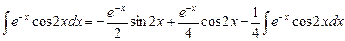 .
.
Выразим искомый интеграл
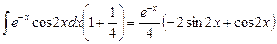 .
.
Тогда 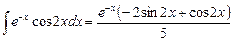 .
.
 2015-06-05
2015-06-05 402
402








