Количеством движения материальной точку называется вектор Q, равный произведению массы m точки на вектор ее скорости 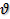 :
:
Q = m 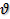
Количество движения механической системы Q, по определению ~ это геометрическая сумма количества движения всех материальных точек, входящих в механическую систему: Q='Lmk•vlc•. Практически количество движения системы удобно находить через ее массу М и скорость 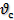 центра масс:
центра масс:
Q = М 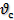
Теорема об изменении количества движения механической системы в инерциальной форме. Производная по времени от количества движения механической системы равна геометрической сумме (главному вектору) всех внешних сил, действующих на систему.
Основы аналитической механики, принцип Даламбера для точки и системы; принцип виртуальных перемещений. Под принципом динамики подразумевается такое аксиоматическое положение, которое обладает общностью и является основным для построения динамики. Тем не менее, в динамике существуют иные принципы, я все они обладают общим свойством: из них логически вытекают уравнения движения и, следовательно, все остальные положения механики, которые получаются из этих уравнений. Разница между различными принципами динамики заключается в большей или меньшей общности и целесообразности их практического применения к исследованию динамики различных механических систем.
Принципы динамики делятся (табл. 4.1) на невариационные и вариационные, на дифференциальные и интегральные. Ниже рассмотрены лишь некоторые дифференциальные принципы динамики.
Таблица 4.1 Классификация принципов динамики
| Принцип динамики | Невариационный | Вариационный |
| Дифференциальный | Общее свойство движения в данный момент времени (принцип Даламбе-ра-п.3.8) | Признак, отличающий истинное движение от других возможных движений в данный момент времени (принцип возможных перемещений - п. 3.9, принцип Даламбера-Лагранжа - п. 3.10) |
| Интегральный | Общее свойство движения за конечный интервал времени | Признак, отличающий истинное движение от других возможных движений за конечный интервал времени |
 2015-06-05
2015-06-05 504
504








