РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ ОТКАЗОВ ТЕХНИЧЕСКОЙ СИСТЕМЫ.
Приведенные выше формулы Бернулли и Пуассона аналитически описывают распределение вероятностей между возможными значениями случайной величины (число отказов элементов TS за единицу времени). Удобно представить эти формулы в виде матрицы, где первая строка содержит возможные значения случайной величины в возрастающем порядке (вариационный ряд), вторая строка − соответствующие им вероятности.
Биномиальное распределение. Распределение Пуассона.
Биноминальное распределение:
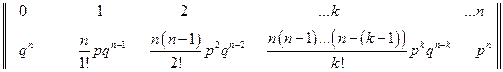 ;
;
Распределение Пуассона:
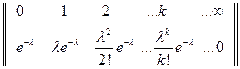 .
.
Пример: TS состоит из трех однородных, независимо работающих элементов. Вероятность отказа каждого элемента за единицу времени равна 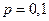 . Составить закон распределения вероятностей случайной величины − число отказавших элементов.
. Составить закон распределения вероятностей случайной величины − число отказавших элементов.
Решение: Вариационный ряд составляют возможные значения случайной величины: 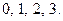 Соответствующие вероятности найдем, учитывая, что
Соответствующие вероятности найдем, учитывая, что 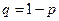 , т.е.
, т.е. 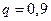 :
:
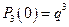 ,
, 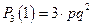 ,
, 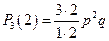 ,
, 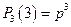
или
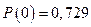 ,
, 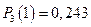 ,
, 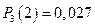 ,
, 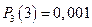 .
.
Таким образом, закон распределения имеет вид:
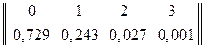 .
.
Критерий правильности вычислений 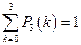 выполняется, т.е.
выполняется, т.е.
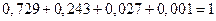 .
.
Пример: TS состоит из 500 однородных, независимо работающих элементов. Вероятность отказа любого элемента в течении установленного времени равна 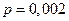 . Составить закон распределения вероятностей случайной величины − число отказавших элементов за установленное время. Найти вероятность того, что за это время откажут:
. Составить закон распределения вероятностей случайной величины − число отказавших элементов за установленное время. Найти вероятность того, что за это время откажут:
1) ровно три элемента;
2) менее трех;
3) более трех;
4) хотя бы один.
Решение: Вариационный ряд составляют возможные значения случайной
величины: 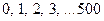 . Соответствующие вероятности найдем по формуле Пуассона, учитывая, что
. Соответствующие вероятности найдем по формуле Пуассона, учитывая, что 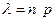 , т.е.
, т.е. 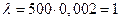 :
:
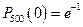 ,
, 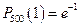 ,
, 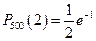 ,
, 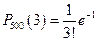 , …
, … 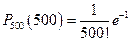
или
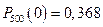 ,
, 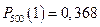 ,
, 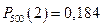 ,
, 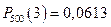 , …
, … 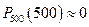 .
.
Таким образом, закон распределения имеет вид:
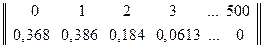 .
.
Откуда непосредственно следует:
1) 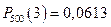 ;
; 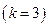 .
.
2) 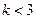 , т.е.
, т.е. 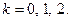
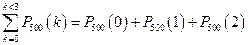
или
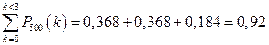 .
.
3) 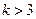 , т.е.
, т.е. 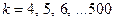 .
. 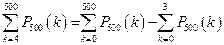 .
.
Учитывая, что 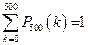 и
и 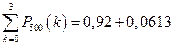 ,
,
получим 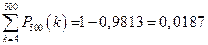 .
.
4) 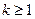 , т.е.
, т.е. 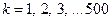 .
. 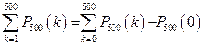
или
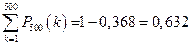 .
.
 2015-06-10
2015-06-10 446
446







