2015-06-26
1267
Системы счисления
г. Могилев 2011
Изучение систем счисления. Методические указания по лабораторной работе №5 по дисциплине «Информатика». Для студентов очной формы обучения специальности 140607 «Электрооборудование автомобилей и тракторов».
Лабораторная работа разработана доцентом кафедры «Электопривод и АПУ»
К.В. Овсянниковым
БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ
Содержание
Системы счисления............................................................................................................................. 1
1 Цель работы...................................................................................................................................... 4
2 Ход работы........................................................................................................................................ 5
2.1 Получение индивидуального задания.................................................................................... 5
2.2 Оформление отчета................................................................................................................... 5
3 Содержание отчета........................................................................................................................... 6
4 Краткие теоретические сведения................................................................................................... 7
4.1 Системы счисления................................................................................................................... 7
4.2 Единицы измерения количества информации.................................................................... 13
4.3 Представление числовой информации................................................................................. 13
5. Задания........................................................................................................................................... 15
4 Контрольные вопросы................................................................................................................... 19
5 Темы для рефератов....................................................................................................................... 20
Литература......................................................................................................................................... 21
Цель работы
Целью лабораторной работы является:
1) изучение среды систем счисления;
2) получение практических навыков по работе с различными системами счисления.
Ход работы
Получение индивидуального задания
Вначале следует получить индивидуальное задание у преподавателя, проводящего лабораторную работу. Варианты заданий приводятся в разделе 5.
Оформление отчета
Отчет оформляется индивидуально каждым студентом..
Содержание отчета
Отчет по лабораторной работе выполняется на листах формата А4. В состав отчета входят:
1) титульный лист;
2) цель работы;
3) текст индивидуального задания;
4) выполнение индивидуального задания.
Краткие теоретические сведения
Системы счисления
Под системой счисления понимается способ представления любого числа с помощью некоторого алфавита символов, называемых цифрами. Системы счисления бывают позиционными и непозиционными.
В позиционных системах счисления значимость (вес) каждой цифры числа зависит от позиции, которую она занимает. Значение числа, состоящего из n цифр, может быть определено следующим образом:
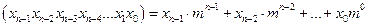
где m — основание системы;
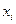, - символ в i -й позиции,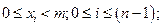 
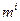- вес i -го знакоместа.
Для десятичной системы счисления m = 10, используемые символы: 0-9.
56310 =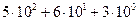 
| I | |||
| xi | |||
| mi | |||
| ximi |
Кроме десятичной системы широкое распространение получили позиционные системы счисления с основаниями 2, 8, 16, 60.
Из непозициоиных систем самой распространенной является римская.
Электронные блоки компьютера могут обрабатывать информацию, представленную только в цифровой форме, причем обычно компьютеры работают в двоичной системе счисления. Основание системы: m = 2. Используемые символы: 1 и 0.
С точки зрения электроники значение единицы может быть представлено наличием напряжения, потенциала или тока, а ноль — отсутствием их.
Рассмотрим представление чисел в двоичной системе. Веса знакомест: 20=1, 21=2, 22 = 4, 23 = 8, 24=16, 25 = 32, 26 = 64, 27 = 128, 28 = 256, 210 = 1024, 216 = 65536.
4.1.1 Перевод числа из десятичной системы в двоичную. Перевод числа из десятичной системы в двоичную осуществляется отдельно для целой и дробной частей числа по следующим алгоритмам:
а) целое десятичное число делится нацело на основание 2, затем на 2 делятся последовательно все частные от целочисленного деления, до тех пор пока частное не станет меньше основания. В результат заносится последнее частное и все остатки от деления, начиная с последнего (рисунок 4.1). 22710= 111000112;
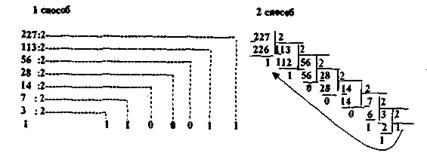
Рисунок 4.1 - Перевод числа из десятичной системы в двоичную
б) десятичная дробь последовательно умножается на основание 2, причем сразу после каждой операции умножения полученная целая часть записывается в результат и в дальнейшем умножении не участвует. Количество операций умножения зависит от требуемой точности, например, 0.6410 = 0.101000112
0.64•2
1.28•2
0.56•2
1.12•2
0.24•2
0.48•2
0.96•2
1.92•2
1.84•2
4.1.2 Перевод числа из двоичной системы в десятичную. Перевод числа из двоичной системы в десятичную можно осуществлять для целой и дробной частей числа по одному алгоритму путем вычисления суммы произведений цифры двоичного числа на вес ее знакоместа:
111000112 = 1•27 + 1•26 + 1•25 + 0•24 + 0•23 + 0•22 + 1•21 + 1•20 = 128 + 64 + 32 + 2 + 1 = 22710
0,101000112 = 1•2-1 + 0•2-2 + 1•2-3 + 0•2-4 + 0•2-5 + 0•2-6 + 1•2-7 + 1•2-8 = 0.5 + 0.125 + 0.0078 + 0.0039 = 0.636710
4.1.3 Представление в компьютере отрицательных чисел. В отличие от десятичной системы в двоичной системе счисления отсутствуют специальные символы, обозначающие знак числа: положительный (+) или отрицательный (-), поэтому для представления двоичных отрицательных чисел используются следующие две формы.
Форма значения со знаком - старший (левый) разряд метится как знаковый и содержит информацию только о знаке числа:
1 — число отрицательное;
0 — число положительное.
Остальные разряды отводятся под абсолютную величину числа.
510 = 0000 01012
-510 = 1000 01012
(Для 8-ми разрядного представления в памяти ПЭВМ)
Форма обратного дополнительного кода, перевод в которую производится по следующему алгоритму:
1. инвертировать все разряды числа, кроме знакового разряда;
2. прибавить единицу к полученному коду;
3. восстановить единицу в знаковом разряде.
Преобразование числа:
-510 = 1000 0101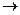 
111 1010 + 1 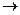111 1011 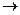1111 1011.
Чаще всего устройство компьютера выполняется таким образом, чтобы отрицательные числа были представлены в дополнительном коде, поскольку это дает существенную экономию времени при выполнении с ними арифметических операций.
Основные свойства дополнительных кодов:
Дополнительный код положительного числа — само число.
Преобразование дополнительного кода по приведенному алгоритму перевода приводит к первоначальному виду числа в знаковой форме.
4.1.4 Правила выполнения арифметических операций в двоичной системе.
Сложение. Операция сложения выполняется так же, как и в десятичной системе. Переполнение разряда приводит к появлению единицы в следующем разряде:
0+0=0,
0+1=1,
1 + 1=10;
| + | |
Вычитание. Вычитание сводится к сложению с отрицательным числом:
15 - 8 =15+ (-8).
Правила вычитания в двоичной системе. Алгоритм операции вычитания путем сложения дополнительных кодов:
1. преобразовать отрицательное число из формы со знаком в дополнительный код;
2. выполнить операцию двоичного сложения над всеми разрядами, включая знаковый, игнорируя единицу переноса из самого высокого разряда;
3. при равенстве единице знакового разряда суммы, что означает получение отрицательного результата в форме дополнительного кода, необходимо перевести результат в знаковую форму, используя второе свойство дополнений.
13 – 15 = 13 + (-15)
1) -1510=10001111 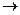1110000+1 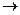1110001 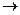11110001
2)
| + | |
3) 1111 1110 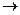000 0001+1 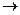1000 0010=210
Таким образом, при выполнении операций сложения и вычитания арифметико-логическому устройству процессора приходится выполнять поразрядное сложение с переносом, инвертирование и проверку на знак двоичных чисел.
В тех случаях, когда необходимо произвести арифметические действия над числами больше 127, они размещаются уже не в одном, а в двух и более регистрах.
Умножение. Если наряду с перечисленными операциями выполнить операции сдвига, то с помощью сумматора можно выполнить и умножение, которое сводится к серии повторных сложений. Если цифра в нулевой позиции множителя равна 1, то множимое переписывается под соответствующими разрядами, умножение на последующие единицы приводят к сдвигу слагаемого влево на одну позицию. Если цифра множителя равна 0, то следующее слагаемое смещается на две позиции влево.
1510•1310=19510=110000112=1•27+1•26+1•21+1•20=19510
| + | |
| + + | |
| 00001111. | |
| 00001111. | |
Деление. При выполнении операции деления несколько раз производится операция вычитания. Поэтому предварительно следует найти дополнительный код делителя. Деление выполняется путем повторного вычитания и сдвига. Для примера выполним деление числа 195 на 15 или в двоичной системе 11000012 на 11112. Дополнительный код числа 1111 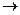11110001. Поскольку по правилам деления каждое промежуточное делимое должно быть больше делителя, выбираем в качестве первого делимого число 11000, т.е. первые пять разрядов и добавляем слева три нуля, дополняя делимое до 8 разрядов. Затем производим сложение его с дополнительным кодом делимого и заносим в результат единицу. Если следующее делимое - после сноса очередной цифры будет меньше делителя, то в результат заносится нуль и в делимое сносится еще одна цифра из исходного делимого.
| + | ||
| + | ||
| + | ||
Делимое 111 - на третьем шаге после сложения и сноски очередного разряда меньше делителя, поэтому записываем в результат 0 и сносим еще один разряд из оставшихся в делимом. После третьего шага результат сложения равен 0, деление закончено.
Ответ: 000011012 = 1310
4.1.5 Использование восьмеричной и шестнадцатеричной систем счисления. Двоичная система счисления неудобна для использования человеком, поэтому программисты используют (использовали) восьмеричную (основание 8, используемые символы 0-7) и шестнадцатеричную (основание 16, используемые символы 0-9, A-F) системы (таблица 4.l).
Таблица 4.1 Позиционные системы счисления
| Десятичная | Двоичная | Восьмеричная | Шестнадцатеричная |
| А | |||
| В | |||
| С | |||
| D | |||
| Е | |||
| F | |||
Каждая тройка двоичных разрядов соответствует одной восьмеричной цифре, а каждая четверка — шестнадцатеричной. Отсюда следует простота преобразований из двоичной системы в восьмеричную и шестнадцатеричную системы счисления.
Например:
110100112 = 1101 00112 = D316
110100112 = 011 010 0112 =3238.
Если исходное количество бит не кратно 3 или 4, добавляются нули слева.
Обратное преобразование аналогично:
В916= 1011 10012
2708 = 10 111 0002.
Перевод из десятичной системы в m-ричную систему счисления производится аналогично переводу в двоичную систему путем целочисленного деления десятичного числа на основание системы т до тех пор, пока частное не станет меньше основания. Так, перевод в 16-ричную систему осуществляется следующим образом:
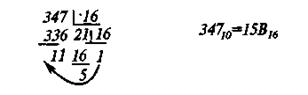
Перевод из m-ричной системы в десятичную систему производится путем сложения произведений соответствующего десятичного эквивалента символа числа в m-ричной системе на вес i -го знакоместа.
Пример перевода из 16-ричной системы счисления в десятичную систему:
15В16 = 1•162 + 5•161 + 11•160 = 256 + 80 + 11 = 34710.
