Лінійна кореляція

Якщо обидві лінії регресії 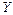на та на 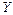– прямі, то кореляцію називають лінійною.

Вибіркове рівняння прямої лінії регресії 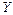на має вигляд

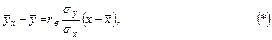
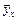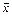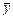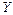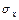де – умовна середня; і – вибіркові середні ознак та ; та 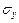– вибіркові середні квадратичні відхилення; 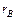– вибірковий коефіцієнт кореляції, причому

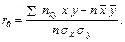
Вибіркове рівняння прямої лінії регресії на 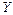має вигляд:

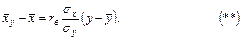
Якщо дані спостереження над ознаками та 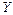задані у вигляді кореляційної таблиці з рівновіддаленими варіантами, то доцільно перейти до умовних варіант

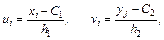
де 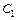– «хибний нуль» варіант 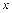(новий початок відліку); в якості хибного нуля вигідно прийняти варіанту, яка розташована приблизно в середині варіаційного ряду (умовимося брати в якості хибного нуля варіанту, яка має найбільшу частоту); 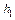– крок, тобто різниця між двома сусідніми варіантами ; 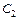– хибний нуль варіант 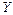; 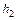– крок варіант .

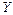У цьому випадку вибірковий коефіцієнт кореляції

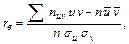
причому доданок 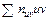зручно обчислювати, використовуючи розрахункову таблицю.

Величини 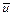, , 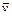, 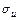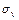можуть бути знайдені або методом добутків (при великому числі даних), або безпосередньо за формулами:

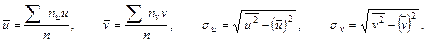
Знаючи ці величини, можна визначити, величин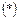и и 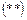, що входять у рівняння регресії за формулами:

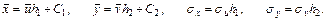
Для оцінки сили лінійного кореляційного зв'язку служить вибірковий коефіцієнт кореляції 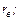чим ближче 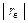до одиниці, тим зв'язок сильніше; чим ближче 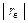до нуля, тим зв'язок слабший.