При решении этой задачи необходимо знать формулы:
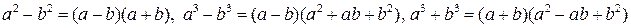
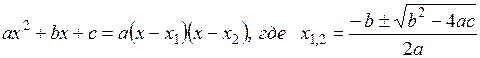 .
.
Пример 2
Вычислить 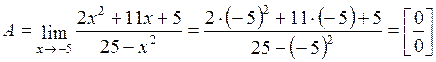
Найдем корни многочлена по формуле 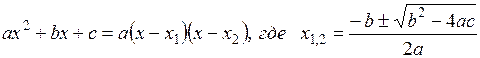 .
.
Тогда 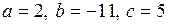 и
и
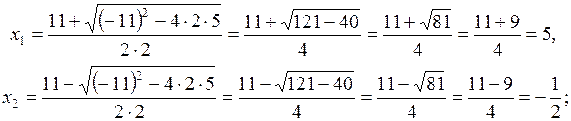
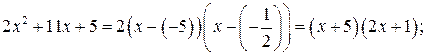
По формуле: 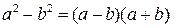 имеем
имеем 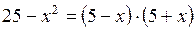
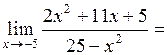
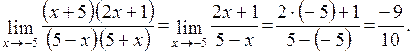
Контрольные варианты к задаче 2
Вычислить пределы функций:
1. 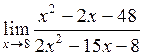 . .
| 2. 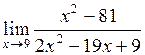 . .
|
3. 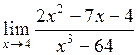 . .
| 4. 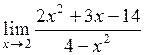 . .
|
5. 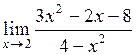
| 6. 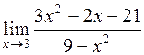 . .
|
7. 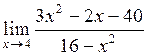
| 8. 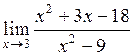
|
9. 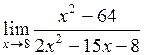
| 10. 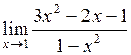
|
11. 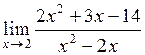
| 12. 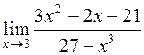 . .
|
13. 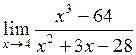
| 14. 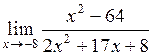 . .
|
15. 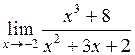 . .
| 16. 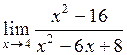 . .
|
17. 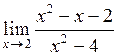 . .
| 18. 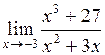 . .
|
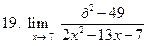 . .
| 20. 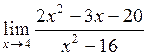 . .
|
21. 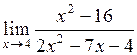 . .
| 22. 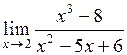 . .
|
23. 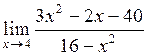 . .
| 24. 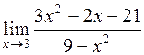 . .
|
25. 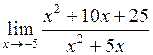 . .
| 26. 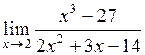 . .
|
27. 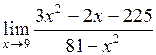 . .
| 28. 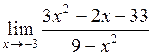 . .
|
29. 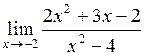 . .
| 30. 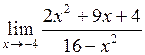
|
З а д а ч а 3
Если при 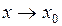
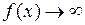 и
и 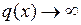 , то отношение
, то отношение 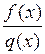 представляет собой неопределенность
представляет собой неопределенность 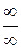 . В этом случае рекомендуется числитель и знаменатель разделить почленно на старшую степень переменной х. При этом необходимо знать, что величина обратная бесконечно большой являетсябесконечно малой
. В этом случае рекомендуется числитель и знаменатель разделить почленно на старшую степень переменной х. При этом необходимо знать, что величина обратная бесконечно большой являетсябесконечно малой 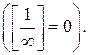 Величина обратная бесконечно малой является бесконечно большой
Величина обратная бесконечно малой является бесконечно большой 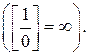
 2015-06-24
2015-06-24 178
178








