В трехмерном пространстве одним из важнейших способов определения плоскости является указание точки на плоскости и вектора нормали к ней.
Допустим, 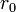 является радиусом-вектором точки
является радиусом-вектором точки 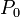 , заданной на плоскости, и допустим, что n - это ненулевой вектор, перпендикулярный к плоскости (нормаль). Идея состоит в том, что точка
, заданной на плоскости, и допустим, что n - это ненулевой вектор, перпендикулярный к плоскости (нормаль). Идея состоит в том, что точка 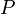 с радиусом-вектором r находится на плоскости тогда и только тогда, когда вектор, проведённый от
с радиусом-вектором r находится на плоскости тогда и только тогда, когда вектор, проведённый от 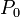 к
к 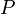 , перпендикулярен n.
, перпендикулярен n.
Вернёмся к тому, что два вектора являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю. Отсюда следует, что нужная нам плоскость может быть выражена как множество всех точек r таких, что:
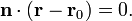 (Здесь точка означает скалярное произведение, а не умножение.)
(Здесь точка означает скалярное произведение, а не умножение.)
Развернув выражение, мы получим:
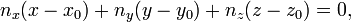
что является знакомым нам уравнением плоскости.
Например: Дано: точка на плоскости 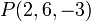 и вектор нормали
и вектор нормали 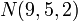 .
.
Уравнение плоскости записывается так:
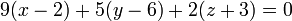
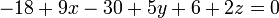
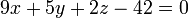
 2015-06-28
2015-06-28 404
404








