Связанные понятия

2 3 4 5 6 7 8

· Угол между двумя плоскостями. Если уравнения П. заданы в виде (1), то

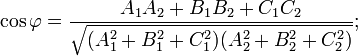
Если в векторной форме, то

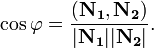
· Плоскости параллельны, ес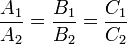ли

или 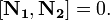(Векторное произведение)

· Плоскости перпендикулярны, ес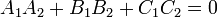ли

или 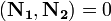. (Скалярное произведение)

· Пучок плоскостей — все плоскости, проходящие через линию пересечения двух плоскостей. Уравнение пучка плоскостей, то есть любой плоскости, проходящей через линию пересечения двух плоскостей, имеет вид^[1]:222:

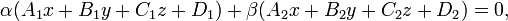
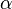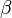где и — любые числа, не равные одновременно нулю. Уравнение самой этой линии можно найти из уравнения пучка, подставляя α=1, β=0 и α=0, β=1.

· Связка плоскостей — все плоскости, проходящие через точку пересечения трёх плоскостей^[1]:224. Уравнение связки плоскостей, то есть любой плоскости, проходящей через точку пересечения трёх плоскостей, имеет вид:

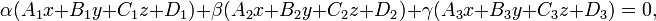
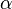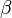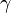где , и — любые числа, не равные одновременно нулю. Саму эту точку можно найти из уравнения связки, подставляя α=1, β=0, γ=0; α=0, β=1, γ=0 и α=0, β=0, γ=1 и решая получившуюся систему уравнений.

[править]m-плоскость в пространстве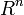

Пусть дано n-мерное аффинный-точененое пространство 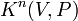, над полем действительных чисел. В нём выбрана прямоугольная система координат 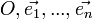. m-плоскостью называется множество точек 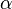, радиус векторы которых удовлетворяют следующему соотношению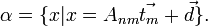 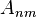- матрица, столбцы которой образует направляющие подпространство плоскости, 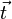- вектор переменных, 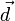- радиус-вектор одной из точек плоскости.
Указанное соотношение можно из матрично-векторного вида перевести в векторный:
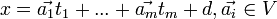- векторное уравнение m-плоскости.
Вектора 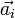образуют направляющее подпространство. Две m-плоскости 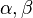называются параллельными, если их направляющие пространства совпадают и .

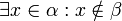(n-1)-плоскость в n-мерном пространстве называется гиперплоскостью или просто плоскостью. Для гиперплоскости существует общее уравнение плоскости. Пусть 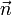- нормальный вектор плоскости, 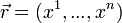- вектор переменных, 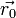- радиус вектор точки, принадлежащей плоскости, тогда:
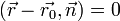- общее уравнение плоскости.
Имя матрицу направляющих векторов, уравнение можно записать так: , или:
.
Углом между плоскостями называется наименьший угол между их нормальными векторами.