Уравнения прямой, проходящей через заданную точку перпендикулярно заданному вектору

ПРЯМАЯ НА ПЛОСКОСТИ

Пусть на координатной плоскости 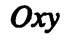(в прямоугольной системе координат) заданы:

а) точка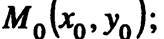

б) ненулевой вектор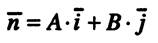
Требуется составить уравнение прямой, проходящей через точку 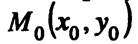перпендикулярно вектору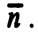

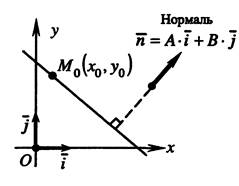
Ненулевой вектор 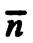, перпендикулярный заданной прямой, называется нормальным вектором (или, короче, нормалью) для этой прямой.

Пусть 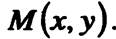произвольная или, как говорят, текущая точка

нашей прямой.Для всех точек этой прямой и только для них характеристическим свойством, определяющим эту прямую, является перпендикулярность векторов .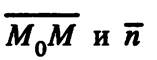

Условие ортогональности запишем при помощи скалярного произведения 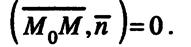Получили векторное уравнение прямой. Найдем координатную форму записи векторного уравнения прямой. Так как, М 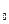M= (x-x 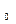)i + (y - y 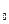)j, 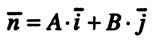,то имеем

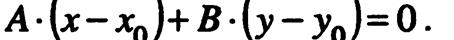
Полученное соотношение позволяет по координатам точки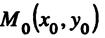

и координатам А, В нормали 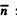записать уравнение прямой без промежу­точных вычислений.

Пример.1 Даны вершины треугольника А(0; 1), B(6; 5), C(12; -1). Найти уравнение высоты, проведенной из вершины С.

Решение. Найдем координаты вектора 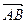, который является вектором нормали к нашей прямой 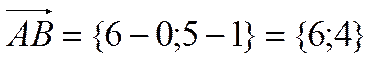.Уравнение высоты:

6(x-12)+4(y+1)=0; 3x+2y-34=0.

2.2. ОБЩЕЕ УРАВНЕНИЕ ПРЯМОЙ.

Задача. Что представляет из себя фигура на плоскости, описываемая уравнением 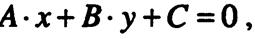(1)

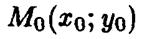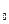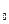Решение. Пусть точка принадлежит нашей фигуре, тогда Ax +By + C 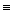0 (2). Вычитая из (1) (2), получим

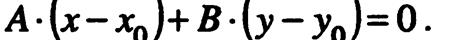(3)

Уравнение (3) получено из (1) тождественным преобразованием,

Поэтому оба уравнения описывают одну и ту же фигуру.Но (3)

описывает прямую линию на плоскости, проходящую через точку 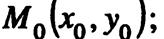перпендикулярно ненулевому вектору

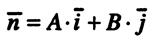.Уравнение (1) называют общим уравнением прямой на плоскости. коэффициенты а и bв общем уравнении прямой имеют простой геометри­ческий смысл. Это координаты вектора, перпендикулярного прямой.