Пусть заданы точка 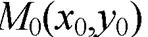 и прямая
и прямая 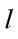 уравнением
уравнением
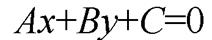
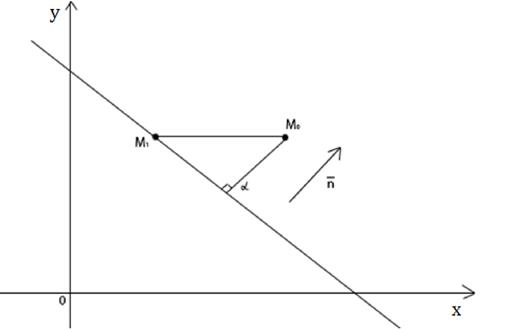
Найдём расстояние 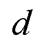 от точки
от точки 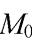 до прямой
до прямой 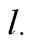 Расстояние
Расстояние 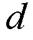 от точки
от точки 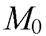 до прямой
до прямой 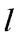 равно длине проекции вектора
равно длине проекции вектора 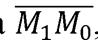 где
где 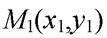 -произвольная точки прямой
-произвольная точки прямой 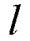 на направление нормального вектора
на направление нормального вектора 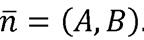 .Значит,
.Значит, 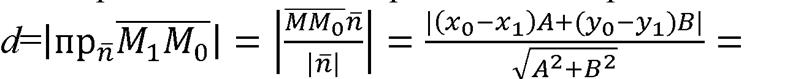
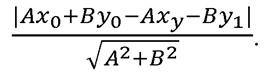
Так как точка 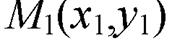 принадлежит прямой
принадлежит прямой 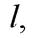 то
то 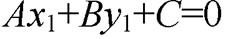 или
или 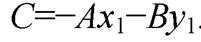 Поэтому
Поэтому
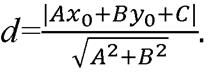
Пример9. Две стороны квадрата лежат на прямых 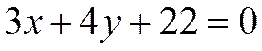 и
и 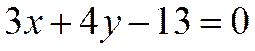 . Вычислить его площадь.
. Вычислить его площадь.
Решение: Из заданных уравнений прямых следует, что они параллельны (коэффициенты 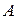 и
и  – одинаковы). Для нахождения длины стороны квадрата нужно найти расстояние от одной прямой до другой. Это можно сделать, взяв точку на одной прямой и определить расстояние от нее до другой прямой. Возьмем первую прямую:
– одинаковы). Для нахождения длины стороны квадрата нужно найти расстояние от одной прямой до другой. Это можно сделать, взяв точку на одной прямой и определить расстояние от нее до другой прямой. Возьмем первую прямую: 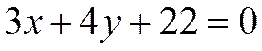 , пусть
, пусть 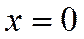 , подставив это значение в уравнение, получим уравнение относительно
, подставив это значение в уравнение, получим уравнение относительно 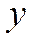 , откуда найдем
, откуда найдем 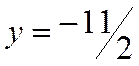 . Таким образом, получим точку, принадлежащую первой прямой:
. Таким образом, получим точку, принадлежащую первой прямой: 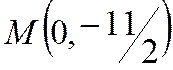 .
.
Расстояние от точки с известными координатами до прямой определяем с помощью формулы: 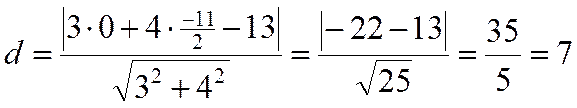 .
.
Теперь определяем площадь: 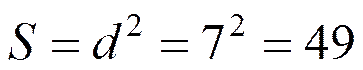 . Ответ:
. Ответ: 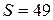 .
.
Пример10. По известным координатам вершин треугольника 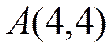 ,
, 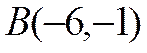 ,
, 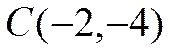 записать для его сторон и биссектрисы угла
записать для его сторон и биссектрисы угла 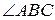 уравнения.
уравнения.
Решение: Так как нам известны координаты вершин, то проще всего получить уравнение сторон в канонической форме.Для канонического уравнения нам нужны координаты точки, принадлежащей стороне и координаты направляющего вектора (параллельного рассматриваемому).
1. Найдем уравнение стороны 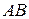 . В качестве точки прямой можно взять точку
. В качестве точки прямой можно взять точку 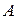 с заданными координатами, а в качестве направляющего вектора – вектор
с заданными координатами, а в качестве направляющего вектора – вектор 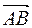 . Найдем координаты вектора
. Найдем координаты вектора 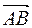 :
:

2. Тогда каноническое уравнение стороны 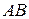 запишется как:
запишется как: 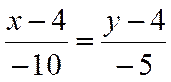 , или
, или 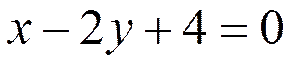 .
.
3. Аналогично можно получить уравнения остальных сторон треугольника: для стороны 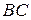 : координаты вектора
: координаты вектора 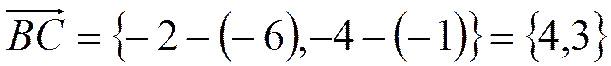 .
.
4. Откуда каноническое уравнение: 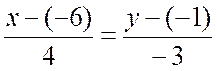 . Следовательно, общее уравнение:
. Следовательно, общее уравнение: 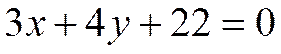 .
.
5. Для стороны 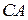 : координаты направляющего вектора
: координаты направляющего вектора 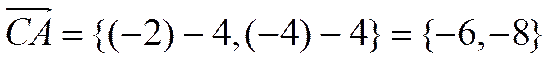 .
.
6. Каноническое уравнение: 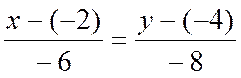 , или
, или 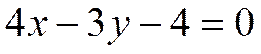 .
.
7. Выведем общее уравнение для биссектрисы. Известно, что биссектриса делит угол пополам. Если на сторонах 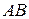 и
и 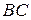 треугольника отложить орты (соответственно
треугольника отложить орты (соответственно 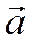 и
и 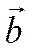 ) и построить на них ромб, то диагональ ромба также поделит угол пополам (по своему свойству) и, значит, ее можно будет взять направляющей биссектрисы. Вектор, построенный на диагонали ромба, равен сумме векторов
) и построить на них ромб, то диагональ ромба также поделит угол пополам (по своему свойству) и, значит, ее можно будет взять направляющей биссектрисы. Вектор, построенный на диагонали ромба, равен сумме векторов  и
и 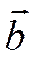 .
.
Для нахождения орта 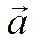 необходимо знать координаты вектора
необходимо знать координаты вектора 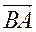 :
:
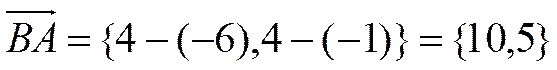 , откуда
, откуда 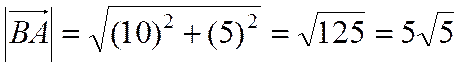 и, соответственно
и, соответственно 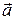 определится как:
определится как:
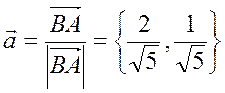 .
.
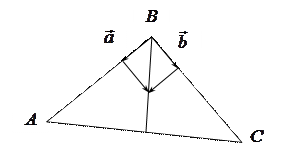
. Иллюстрация решения задачи
8. Аналогично определим орт 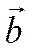 :
:
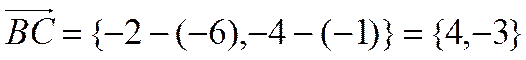 ;
; 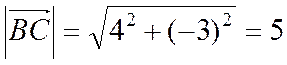 ;
;
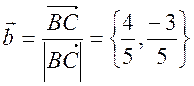 . Теперь определим их сумму:
. Теперь определим их сумму:
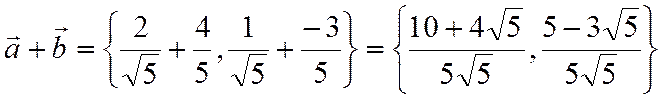 .
.
9. Тогда каноническое уравнение биссектрисы:

 .
.
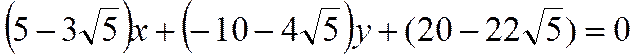 .
.
Пример11. Определить координаты точки, симметричной точке М 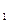 (-1;0) относительно прямой х-3у+6=0.
(-1;0) относительно прямой х-3у+6=0.
Решение. Симметричная точка относительно прямой
х-3у+6=0 лежит на перпендикуляре к этой прямой, который проходит через точку М(-1; 0), следовательно, нам нужно составить уравнение этого перпендикуляра. Угловой коэффициент заданной прямой k= 1/3, поэтому угловой коэффициент перпендикуляра k=-3 и его уравнение y-0=-3(x+1),
y+3x+3=0.Теперь находим координаты точки пересечения P прямой х-3у+6=0 и перпендикуляра y+3x+3=0. Для этого решим систему уравнений:
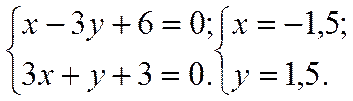 P(-1,5;1,5).
P(-1,5;1,5).
Пусть M 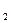 (x
(x 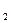 ;y
;y 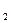 )-точка симметричная точке М
)-точка симметричная точке М  относительно данной прямой. Точка P расположена посредине отрезка М
относительно данной прямой. Точка P расположена посредине отрезка М 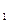 М
М 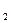 , поэтому можно использовать формулы координат средины отрезка:
, поэтому можно использовать формулы координат средины отрезка:
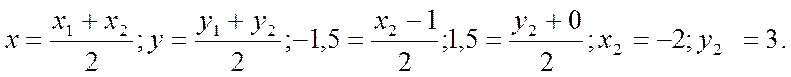 Ответ: М
Ответ: М  (-2; 3).
(-2; 3).
 2015-06-28
2015-06-28 710
710







