Если на плоскости хоу заданы две прямые с известными угловыми коэффициентами 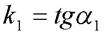 и
и 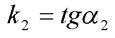 , то можно найти угол
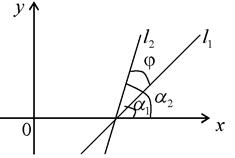
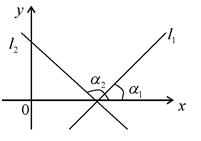
, то можно найти угол 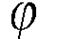 между этими прямыми, как угол, на который нужно повернуть против часовой стрелки прямую 1 до ее совпадения с прямой 2
между этими прямыми, как угол, на который нужно повернуть против часовой стрелки прямую 1 до ее совпадения с прямой 2
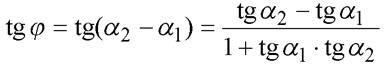 или
или
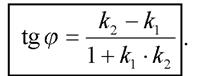
Параллельность прямых 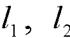 равносильна равенству углов наклона
равносильна равенству углов наклона 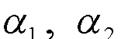 и, следовательно, равенству угловых
и, следовательно, равенству угловых
коэффициентов 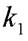 и
и 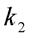 :
: 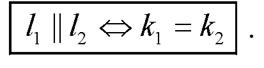
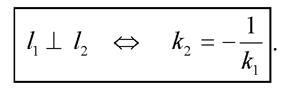
Для перпендикулярных прямых 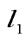 и
и  имеем
имеем 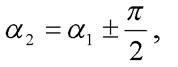
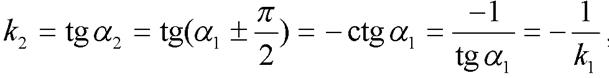
Если прямые 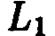 и
и 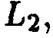 заданы с помощью их общих уравнений
заданы с помощью их общих уравнений 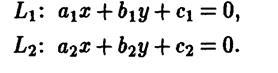
для параллельности прямых 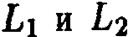 необходимо и достаточно, чтобы были коллинеарными их нормальные векторы
необходимо и достаточно, чтобы были коллинеарными их нормальные векторы 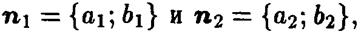 а коллинеарность векторов равносильна пропорциональности их координат. Поэтому
а коллинеарность векторов равносильна пропорциональности их координат. Поэтому 
Так как последнее равенство преобразуется в соотношение 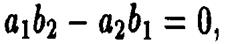 то полученное условие параллельности двух прямых можно записать при помощи определителя второго порядка:
то полученное условие параллельности двух прямых можно записать при помощи определителя второго порядка:
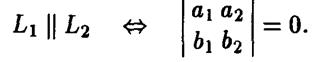
Прямые 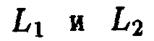 перпендикулярны тогда и только тогда, когда ортогональны их нормальные векторы. Условие ортогональности нормальных векторов
перпендикулярны тогда и только тогда, когда ортогональны их нормальные векторы. Условие ортогональности нормальных векторов 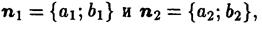 эквивалентно равенству нулю их скалярного произведения
эквивалентно равенству нулю их скалярного произведения 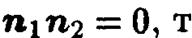 .е., условию
.е., условию 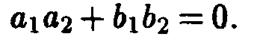
Пример6. Определить угол между прямыми: y = -3x + 7; y = 2x + 1.
Решение.k1 = -3; k2 = 2 tgj = 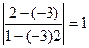 ; j = p/4.
; j = p/4.
Пример7. Составить уравнение прямой, проходящей через точку 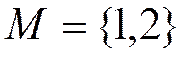 параллельно прямой
параллельно прямой 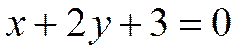 .
.
Решение:1способ. Так как искомая прямая по условию задачи должна быть параллельной исходной, это значит, что они имеют одинаковые угловые коэффициенты. Записав уравнение заданной прямой в виде с угловым коэффициентом y=-0,5x-1,5, находим 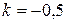 . Записав уравнение заданной прямой в виде с угловым коэффициентом y=-0,5x-1,5, находим
. Записав уравнение заданной прямой в виде с угловым коэффициентом y=-0,5x-1,5, находим 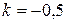 . Обозначим координаты точки
. Обозначим координаты точки 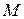 как
как 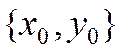 , имеем
, имеем 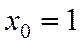 ,
, 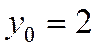 ; прямую, проходящую через эту точку, можно описать уравнением с угловым коэффициентом; подставим в него известные значения, получим:
; прямую, проходящую через эту точку, можно описать уравнением с угловым коэффициентом; подставим в него известные значения, получим: 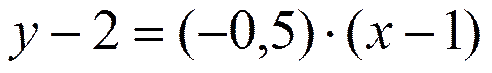 . Проведя несложные преобразования, получим искомое уравнение:
. Проведя несложные преобразования, получим искомое уравнение: 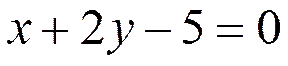 .
.
2 способ.
Прямые должны быть параллельны, это значит, первые два коэффициента в общем уравнении у них должны быть одинаковы, следовательно уравнение нашей прямой x+2y+c=0, нужно найти только значение свободного члена 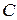 ; из условия принадлежности точки
; из условия принадлежности точки 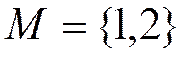 нашей прямой получим 1+2.2+с=0 или с=-5
нашей прямой получим 1+2.2+с=0 или с=-5
Имеем искомое уравнение: 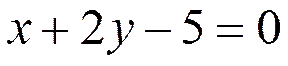 .
.
Пример8. Составить уравнение прямой, проходящей через точку 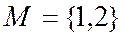 перпендикулярно прямой
перпендикулярно прямой 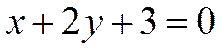 .
.
Решение: 1способ. Записав уравнение заданной прямой в виде с угловым коэффициентом y=-0,5x-1,5, находим 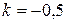 . Из условия перпендикулярности прямых найдем угловой коэффициент искомой прямой k=2. Обозначим координаты точки
. Из условия перпендикулярности прямых найдем угловой коэффициент искомой прямой k=2. Обозначим координаты точки 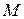 как
как 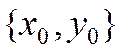 , имеем
, имеем 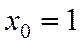 ,
, 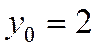 ; прямую, проходящую через эту точку, можно описать уравнением с угловым коэффициентом; подставим в него известные значения, получим:
; прямую, проходящую через эту точку, можно описать уравнением с угловым коэффициентом; подставим в него известные значения, получим: 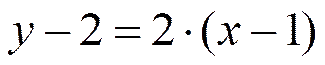 .или:
.или: 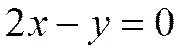
2 способ. Вектор нормали прямой данной в условии задачи
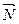 ={1;2} является направляющим вектором искомой прямой
={1;2} является направляющим вектором искомой прямой
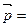 {1;2}. Обозначим координаты точки
{1;2}. Обозначим координаты точки 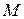 как
как 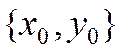 , имеем
, имеем 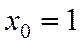 ,
, 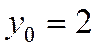 ; Имеем каноническое уравнение
; Имеем каноническое уравнение 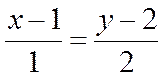 , или:
, или: 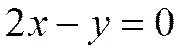 .
.
 2015-06-28
2015-06-28 2881
2881
