Уравнение прямой на плоскости с угловым коэффициентом

Рассмотрим прямую на плоскости. Пусть 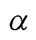- угол наклона прямой к оси 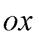Тогда направляющий вектор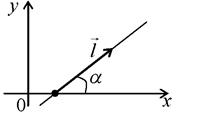 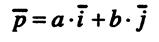=l единичной длины имеет координа­ты a = 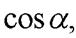иb= 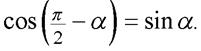Поэтому каноническое уравнение прямой примет вид: 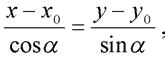или 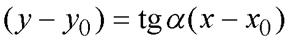. Число есть угловой коэффициент прямой. Таким образом получили, уравнение прямой на плоскости, проходящей через точку в направлении задаваемомугловым коэффи­циентом k имеет вид:

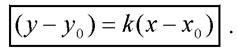
Пример5. Найти уравнение прямой, проходящей через точку

А(-3;4),пересекающей ось OXпод углом = .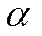

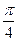Решение. Так как k=1,то наше уравнение y-4=x+3,x-y+7=0.