2015-06-28
2335
Для молекул с различным соотношение величин главных моментов инерции квантование вращательной энергии описывается по разному.
Все многообразие молекул может быть разделено на следующие типы:
Линейные молекулы
Сферические волчки
Симметричные волчки
Асимметричные волчки
Линейные молекулы
Вращение происходит относительно оси, перпендикулярной оси молекулы (примем ось молекулы за z).
Момент инерции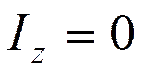 
, а относительно любой перпендикулярной к ней оси моменты одинаковы,
.
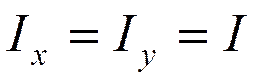Для нелинейных молекул все три момента инерции отличны от нуля.
Возможны три случая:
1. Молекулы типа сферического волчка:
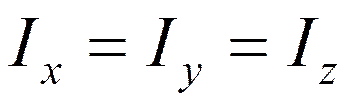
Несколько осей симметрии порядка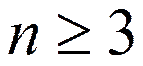 
(CH4, CCl4, UF6)
2. Симметричные волчки.
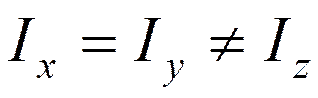
Ось симметрии порядка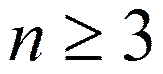 
(относительно всех перпендикулярных к ней осей моменты одинаковы)
(NH3, FCH3, C6H6) 
Обозначим главные моменты инерции IA, IB, IC, причем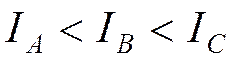 
,
то для симметричного волчка возможны варианты:
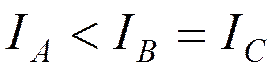- вытянутый волчок;
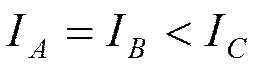- сплюснутый волчок
3. Асимметричные волчки
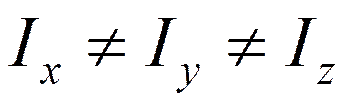
Молекулы с осями симметрии 
- асиметричные волчки (вода и огромное множество других несимметричных молекул)
Вращательные уровни и переходы для линейной молекулы.
|
|
|
Энергия вращения (кинетическая энергия ядер):
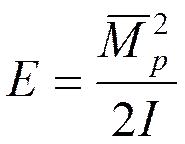(4)
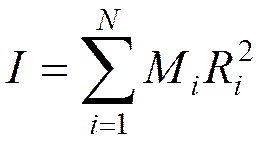, где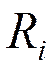 
отсчитываются от центра масс.
Подставляя (2)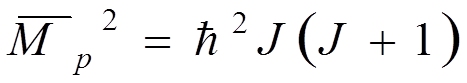 
, получаем 
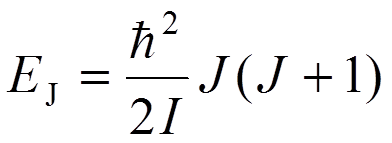(5)
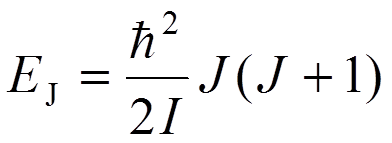
Обозначим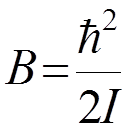 
- вращательная постоянная (6)
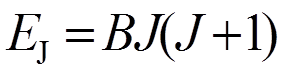(7)
Значения Е J линейной молекулыв зависимости от J
| Е J | 2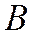 
| 6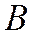
| 12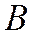
| 20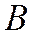
| 30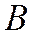
| 42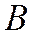
| 56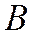
| 72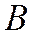
| |
| J |
Расстояния между соседними уровнями возрастают с ростом J:
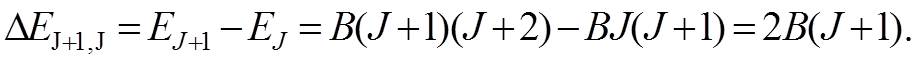
(8)
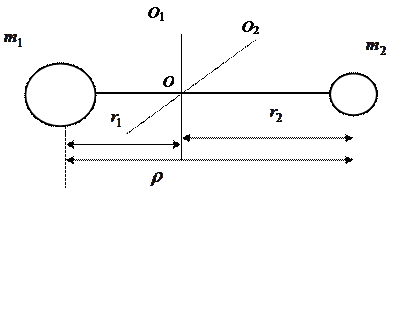
Для важнейшего случая двухатомной молекулы
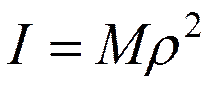(9)
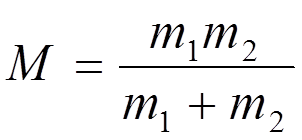- приведенная масса молекулы (10)
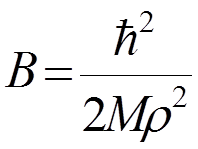(11)
Из анализа вращательного спектра находится В, а затем из (11) - межъядерное расстояние.
Вращательные постоянные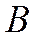 
, межъядерные расстояния ρ
