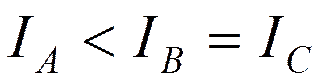Вращательные уровни энергии и спектры молекул типа симметричного волчка

- вытянутый волчок (FCH₃)

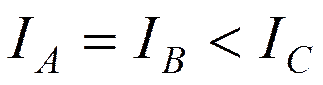- сплюснутый волчок (C₆H₆)

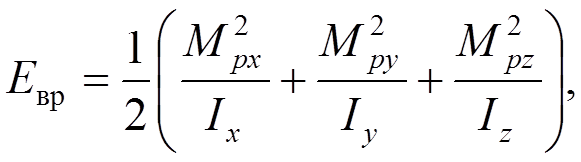
Перепишем, с учетом 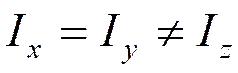и добавив и вычтя :

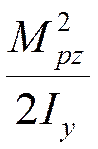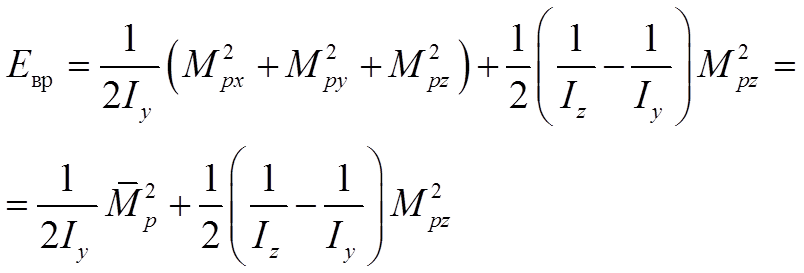. (21)

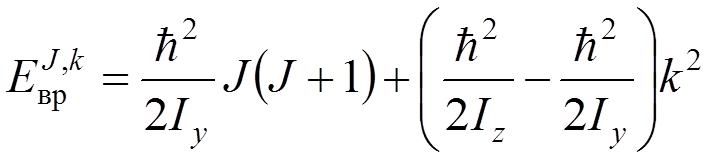. (22)

()
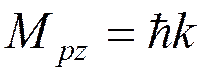Для вытянутого волчка момент инерции относительно «отличающейся» оси z является наименьшим, т.е. .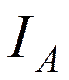

Обозначим вращательные постоянные ,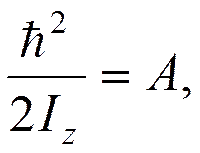

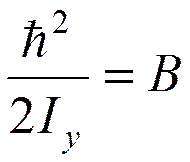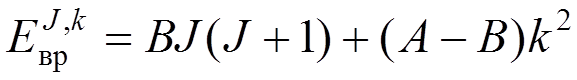(А>В), (23)

(J= 0, 1, 2,...; k = 0, ±1, ±2,... ).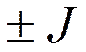

Для сплюснутого волчка ось z является осью наибольшего момента инерции I_C

Здесь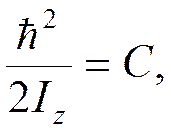

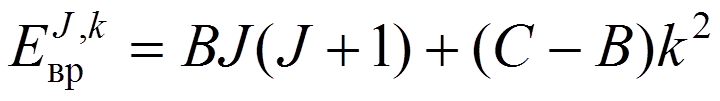, (C < B) (24)

(J = 0, 1, 2,...; k = 0, ±1, ±2,... ).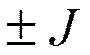

В обеих формулах вращательная постоянная B соответствует моменту инерции относительно осей, перпендикулярных оси симметрии.

Энергия зависит от J и .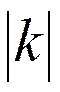

Каждый уровень с заданным J и 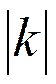в дополнение к вырождению кратности

2 J + 1 (за счет m_J) вырожден за счет того, что положительное и отрицательное k дают одно значение энергии.

Общая кратность вырождения равна 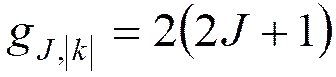, за исключением k =0, для которого она равна 2 J + 1.

Расстояние между уровнями с различными k (при заданном J) зависит для вытянутого волчка от величины А – В, а для сплюснутого волчка от величины С – В.

Для дипольного поглощения и испускания и для спектров КР справедливо правило отбора D k = 0.

Поэтому

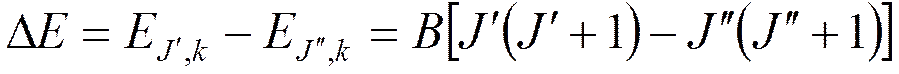
не зависит от k.

В поглощении и испускании D J = ±1 и

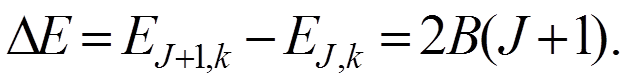
Для КР:

D J = ±1, ±2, что дает две серии линий:

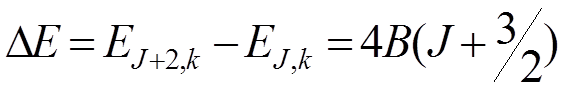
для D J = ±2 (J = 0, 1, 2,...)

и

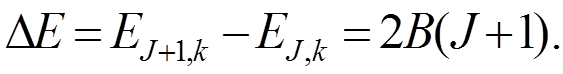
для D J = ±1 (J = 1, 2,...) (Переход 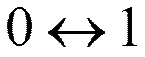запрещен)

Линии с частотами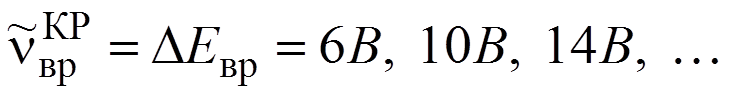

от первой серии накладываются через одну на расположенные вдвое чаще

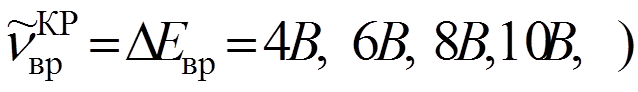( линии второй серии, что дает чередование интенсивностей.

Чисто вращательными спектрами поглощения обладают только дипольные молекулы типа симметричных волчков,

а спектрами КР- все.