Условие  -сти прямых:
-сти прямых: 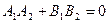 ;
; 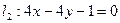 , А(2,1);
, А(2,1); 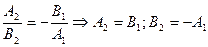 ;
; 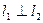 ;
; 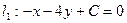 ; -2-4+С=0
; -2-4+С=0 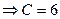 ;
; 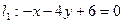 Ответ: -x-4y+6=0
Ответ: -x-4y+6=0
4. Написать уравнения прямой, параллельной данной прямой, и расположенной от нее на заданном расстоянии.
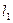 ||
|| 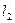
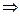
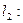 4x+2y+c=0
4x+2y+c=0

А(x,y) 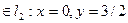 .
.
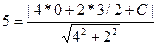 ;
;
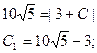
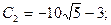
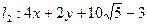 ;
;
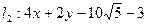
№5.Написать уравнение прямой, проходящей через две заданные точки. Пусть прямая l заданная уравнением с прямым коэффициентом проходящая через две точки 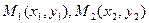 . Так как прямая проходящая через точку М, то можно использовать уравнение проходящее через данную точку
. Так как прямая проходящая через точку М, то можно использовать уравнение проходящее через данную точку 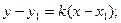 Так как переменная проходящая через точку М
Так как переменная проходящая через точку М 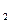 , то координаты М
, то координаты М 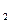 должны удовлетворять уравнению прямой:
должны удовлетворять уравнению прямой: 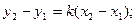
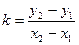 ;
; 
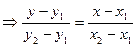 - Ур-ие проходящее через две точки.
- Ур-ие проходящее через две точки.
№7. Найти угол между пересекающимися прямыми. 1) Пусть прямые заданы общими уравнениями: 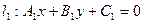 ;
; 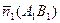
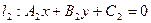 ;
; 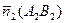 . За угол между прямыми можно принять угол между нормальными векторами этих прямых, а угол между векторами можно определить из скалярного произведения этих векторов:
. За угол между прямыми можно принять угол между нормальными векторами этих прямых, а угол между векторами можно определить из скалярного произведения этих векторов: 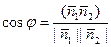 Переходя к координатам векторов получим:
Переходя к координатам векторов получим: 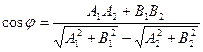 ;
;
П-р: 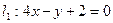 ;
; 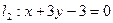 ;
; 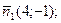
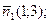
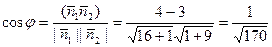
Ответ: 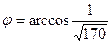
№8. Написать уравнение эллипса, если заданы полуоси и центр. Сделать чертеж. Опр: Эллипс- множество точек в координатной плоскости, сумма расстояния от которого до двух данных точек есть величина постоянная. Данные или фиксированные две точки наз-тся фокусами, обозначаются 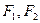 . Каноническое уравнение:
. Каноническое уравнение: 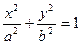 , а- большая полуось, b-малая полуось. Точки с координатами: (а;0),(0;b),(-a;0),(0;-b)- называются вершинами эллипса. Расстояние от начала координат до фокуса обозначают через с, причем
, а- большая полуось, b-малая полуось. Точки с координатами: (а;0),(0;b),(-a;0),(0;-b)- называются вершинами эллипса. Расстояние от начала координат до фокуса обозначают через с, причем 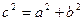 , тогда фокусы имеют след-ие координаты:
, тогда фокусы имеют след-ие координаты: 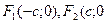 ). Фокальными радиусами точки наз-ся расстояние от точки на гиперболе до фокусов: MF
). Фокальными радиусами точки наз-ся расстояние от точки на гиперболе до фокусов: MF 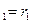 ; MF
; MF 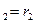 . Директрисами наз-ся прямые перпендикулярные О
. Директрисами наз-ся прямые перпендикулярные О 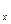 и симметричные относительно О
и симметричные относительно О  . Директрисы задаются ур-ем:
. Директрисы задаются ур-ем: 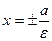 ; Эксинтриситет:
; Эксинтриситет: 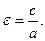 П-р:
П-р: 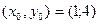 - центр; а=2,
- центр; а=2, 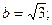
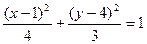
№9. Написать уравнение гиперболы, если заданы полуоси и центр. Сделать чертеж. Найти уравнение асимптот. Гиперболой наз-ся множество точек координатной плоскости для которой модуль разности расстоянии до двух фиксированных точек есть величина постоянная. или фиксированные две точки наз-тся фокусами, обозначаются 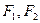 . Каноническое уравнение:
. Каноническое уравнение: 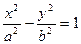 , а- действительная полуось, b-мнимая полуось. Прямоугольник образованный действительной осью и мнимой осью наз-тся основным прямоугольником гиперболы(со сторонами 2аи 2b). Диагонали основного прямоугольника образуют асимптоты гиперболы. Гипербола имеет две вершины: (-а;0),(а;0). Фокальными радиусами точки наз-ся расстояние от точки на гиперболе до фокусов: MF
, а- действительная полуось, b-мнимая полуось. Прямоугольник образованный действительной осью и мнимой осью наз-тся основным прямоугольником гиперболы(со сторонами 2аи 2b). Диагонали основного прямоугольника образуют асимптоты гиперболы. Гипербола имеет две вершины: (-а;0),(а;0). Фокальными радиусами точки наз-ся расстояние от точки на гиперболе до фокусов: MF 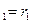 ; MF
; MF 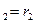 . Расстояние от начала координат до фокуса обозначают через с, причем
. Расстояние от начала координат до фокуса обозначают через с, причем 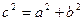 , тогда фокусы имеют след-ие координаты:
, тогда фокусы имеют след-ие координаты: 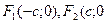 ). Директрисами наз-ся прямые перпендикулярные О
). Директрисами наз-ся прямые перпендикулярные О 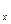 и симметричные относительно О
и симметричные относительно О 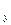 . Директрисы задаются Ур-ем:
. Директрисы задаются Ур-ем: 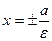 ; Эксинтриситет:
; Эксинтриситет: 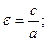 Асимптоты выражаются ур-ем:
Асимптоты выражаются ур-ем: 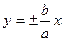 П-р:
П-р: 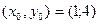 - центр; а=2,
- центр; а=2, 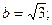
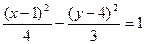
№11. Определить тип кривой второго порядка. Привести Ур-ие к каноническому виду. 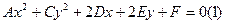 . Если в уравнениях эллипса, гиперболы и параболы все слагаемые перенести в одну часть и избавиться от знаменателя, то можно получить уравнение вида(1). Для такого уравнения справедлива теорема: 1)Если А=С, то Ур-ие (1) определяет окружность; 2) Если А*С>0, то (1) определяет эллипс; 3)Если А*С<0, то (1) определяет гиперболу;4) Если А=0 или С=0, то (1) определяет параболу.
. Если в уравнениях эллипса, гиперболы и параболы все слагаемые перенести в одну часть и избавиться от знаменателя, то можно получить уравнение вида(1). Для такого уравнения справедлива теорема: 1)Если А=С, то Ур-ие (1) определяет окружность; 2) Если А*С>0, то (1) определяет эллипс; 3)Если А*С<0, то (1) определяет гиперболу;4) Если А=0 или С=0, то (1) определяет параболу.
| тип | Название | Каноническое уравнение |
| Эллип- | Эллипс | 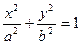 , , 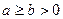 |
| тичес- | «мнимый эллипс» | 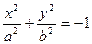 |
| кий | Пара мнимых пересек-щихся прямых | 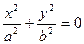 |
| Гипер- | гипербола | 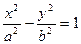 |
| боличес- кий | Пара пересекающихся прямых | 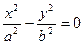 |
| Пара- | парабола | 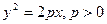 |
| боли- | Пара параллельных прямых | 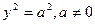 |
| чес- | Пара мнимых паралл-ых прямых | 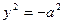 |
| кий | Пара совпадающих прямых | 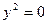 |
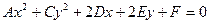 . Если 1)А=С-окружность; 2) А*С>0- эллиптический вид;3)A*C<0-гиперболический тип;4) А=0 или С=0- параболический вид. Пример: 9
. Если 1)А=С-окружность; 2) А*С>0- эллиптический вид;3)A*C<0-гиперболический тип;4) А=0 или С=0- параболический вид. Пример: 9 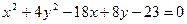 ; А*С=9*4=36>0- эллиптический вид.
; А*С=9*4=36>0- эллиптический вид. 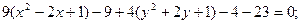
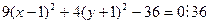 ;
; 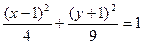 - эллипс; Полуоси a=2,b=3 с центром в точке 1 и -1.
- эллипс; Полуоси a=2,b=3 с центром в точке 1 и -1.
Когда 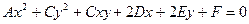
1) 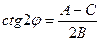 ;2)
;2) 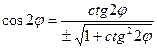 ;3)
;3) 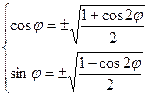 ;4)
;4) 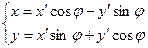
В случае А=С поворот берем 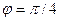 . П-р:
. П-р: 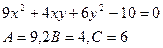

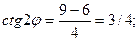
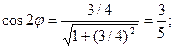

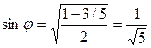 ;
; 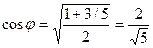 ;
;
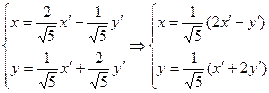 ;
; 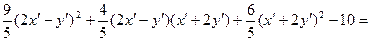
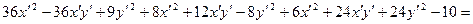
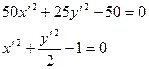 ;
;
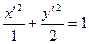 -эллипс в центре (0,0);
-эллипс в центре (0,0); 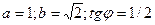 -угол поворота.
-угол поворота.
 2015-06-28
2015-06-28 2404
2404