1. Напишите уравнение плоскости, проходящей через три точки 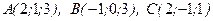 .
.
2. Напишите уравнение плоскости, проходящей через ось 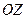 , и через точку
, и через точку 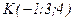 .
.
3. Записать уравнение плоскости, параллельной оси 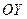 и проходящей через точки
и проходящей через точки 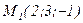 и
и 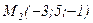 .
.
4. Укажите правильное соответствие между уравнениями и типами уравнений плоскости:
1) 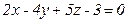 ; 2)
; 2) 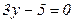 ;
;
3) 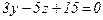 ; 4)
; 4) 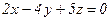 .
.
5) 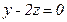 .
.
Варианты ответов:
1) уравнение плоскости, параллельной оси 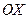 ;
;
2) уравнение плоскости, параллельной плоскости 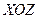 ;
;
3) уравнение плоскости, проходящей через начало координат;
4) уравнение плоскости, содержащей ось 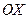 ;
;
5) уравнение плоскости, не содержащей начала и пересекающей все координатные оси.
5. Установите, какие из следующих пар уравнений определяют параллельные плоскости:
1) 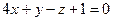 и
и 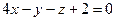 ;
;
2) 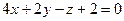 и
и 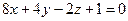 ;
;
3) 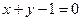 и
и 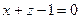 .
.
6. Найдите расстояние между параллельными плоскостями 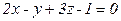 и.
и. 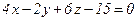 .
.
7. Запишите уравнения прямой, проходящей через точку 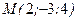 и параллельной прямой
и параллельной прямой 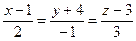 .
.
8. На прямой 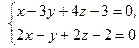 найдите точку, абсцисса которой равна нулю.
найдите точку, абсцисса которой равна нулю.
9. Вершинами треугольника являются точки 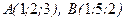 ,
, 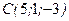 . Запишите уравнения медианы
. Запишите уравнения медианы 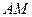 .
.
Пример
1.Записать уравнение плоскости, параллельной оси 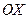 и проходящей через точки
и проходящей через точки 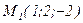 и
и 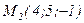 .
.
Решение. Так как искомая плоскость параллельна оси 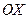 , то вектор, перпендикулярный к этой плоскости, является перпендикулярным к вектору
, то вектор, перпендикулярный к этой плоскости, является перпендикулярным к вектору 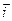 и перпендикулярным к вектору
и перпендикулярным к вектору 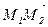 . Таким вектором является, например, вектор
. Таким вектором является, например, вектор 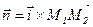 .
.
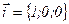 ,
, 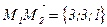 . Найдем
. Найдем 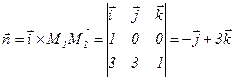 .
.
Уравнение плоскости, проходящей через точку 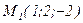 и перпендикулярно вектору
и перпендикулярно вектору 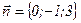 , имеет вид:
, имеет вид: 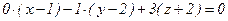 , откуда
, откуда 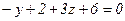 , или
, или 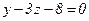 (полученное уравнение плоскости, параллельной оси
(полученное уравнение плоскости, параллельной оси 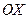 , не содержит явно
, не содержит явно 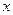 ).
).
 2015-06-28
2015-06-28 1590
1590