П.2. Уравнение плоскости в пространстве

Общее уравнение плоскости: ,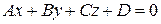

где A, B, C – координаты вектора нормали вектора 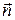(любого вектора, перпендикулярного данной плоскости), D – свободный член уравнения.

Уравнение плоскости, проходящей через точку 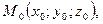перпендикулярно вектору :

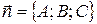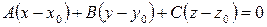. (48)

Уравнение плоскости, проходящей через три заданные точки :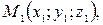

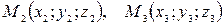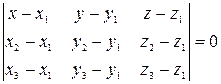. (49)

Угол 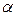между двумя плоскостями, заданными уравнениям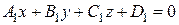и и 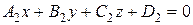определяется как угол между векторами их нормале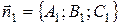й и 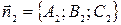или дополнительный к нему (обычно берется острый угол), то есть

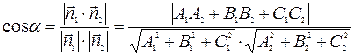. (50)