Возведем это уравнение в квадрат

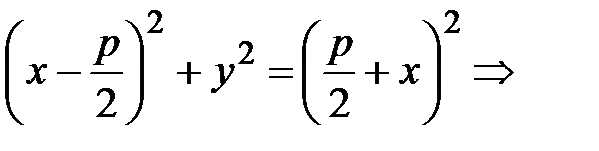
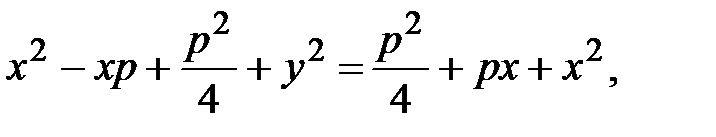
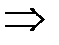
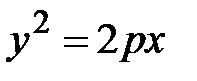
– каноническое уравнение параболы, симметричной относительно оси Оx и проходящей через начало координат.

(20)

– каноническое уравнение параболы, симметричной относительно оси Оx и проходящей через начало координат.

Точка (0; 0) – вершина параболы. Если р > 0 (р < 0), то парабола (20) расположена правее (левее) оси Оу.

Т. к. для параболы 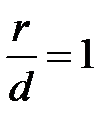, а для эллипса и гиперболы 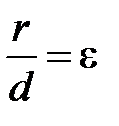, то, следовательно, эксцентриситет параболы =1 (e = 1).

Заметим, что парабола, симметричная относительно Оу и проходящая через начало координат, определяется уравнением х ² = 2 q y (21)

Фокус этой параболы находится в точке 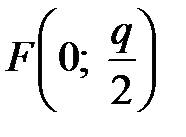. Уравнение ее директрисы 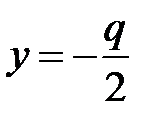. Фокальный радиус ее точки М (х, у) выражается формулой .

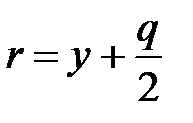Если q > 0 (q < 0), то ветви параболы (21) расположены выше (ниже) оси Ох.

Вопрос 24. Гипербола и её основные свойства.

Гипербола - множество точек плоскости, для каждой из которых модуль разности расстояний от которых до двух данных точек 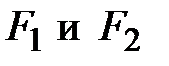той же плоскости, называемых фокусами гиперболы, есть заданная постоянная величина 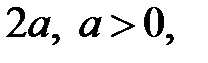меньшая, чем расстояние между фокусами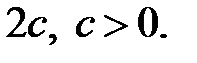

Пусть фокусы гиперболы лежат на оси Ох, причем 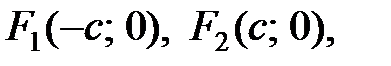т.е. 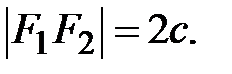Заметим, что

Пусть 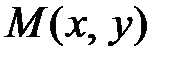– произвольная точка гиперболы. Как и ранее, 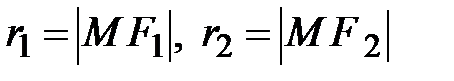– фокальные радиусы точки М.

По определению гиперболы:

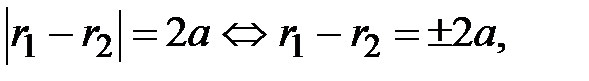где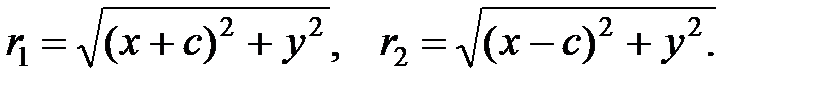

Следовательно, 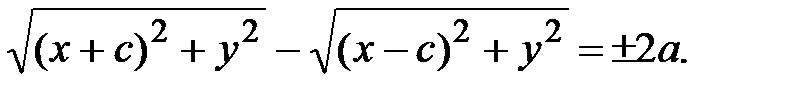(10)

Умножим (10) на 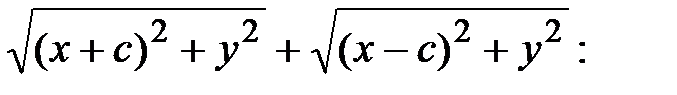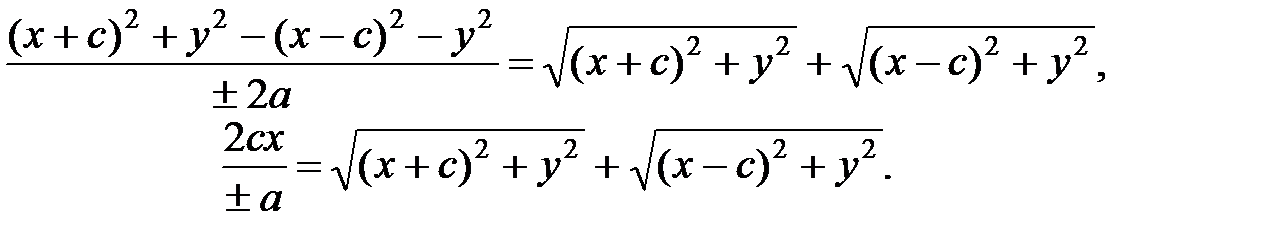(11)

Сложим уравн ени я (10) и (11): 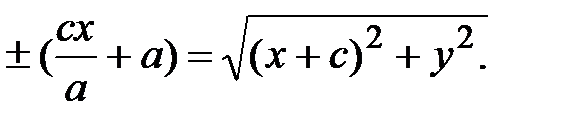(12)

Возведем (12) в квадрат: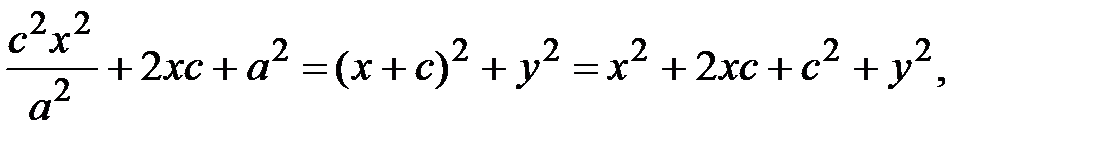

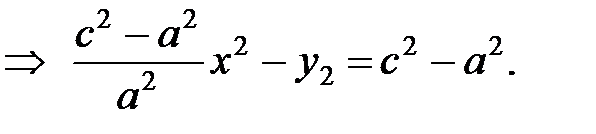
Пусть 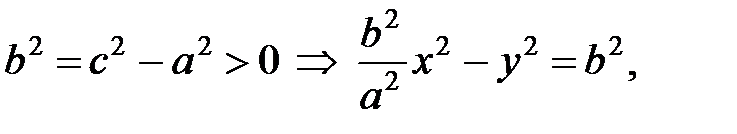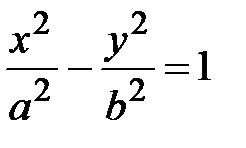(13)

(13)

(13) – каноническое уравнение гиперболы с центром в начале координат.

Соответственно, уравнение 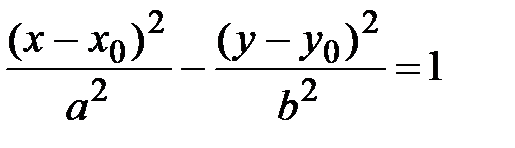– каноническое уравнение гиперболы с центром в точке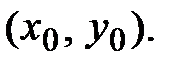

Числа a и b называются соответственно действительной и мнимой полуосями гиперболы. Гипербола с равными полуосями (a=b) называется равносторонней, ее каноническое уравнение имеет вид: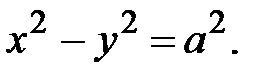

Точки 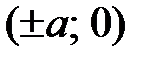называются вершинами гиперболы.

Заметим, что если уравнение гиперболы имеет вид 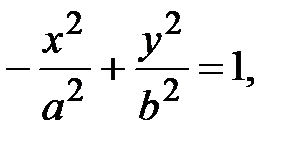(14)

то фокусы гиперболы находятся на оси Оу, а ветви гиперболы будут направлены не влево и вправо, а вверх и вниз.

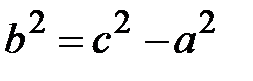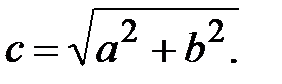Так как , то (15)

Как и в случае с эллипсом, эксцентриситетом гиперболы 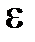называется отношение межфокусного расстояния 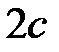к длине действительной оси 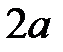: 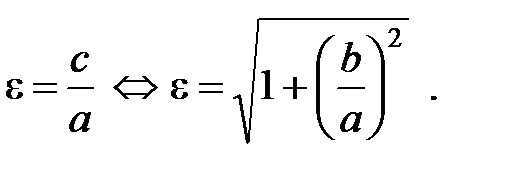(16)

Следовательно,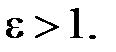

Выразим фокальные радиусы точки 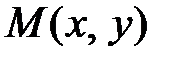через эксцентриситет. Из (12)

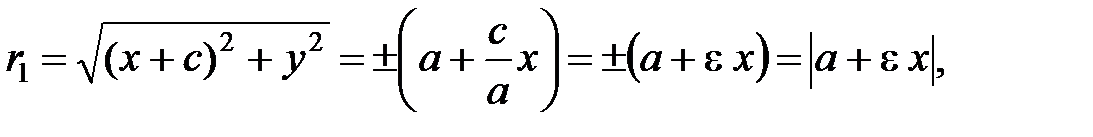
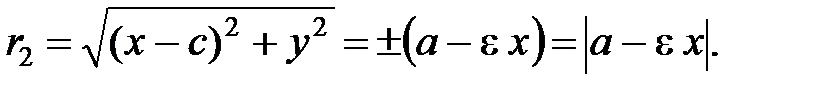(17)

Прямые 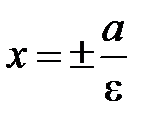называются директрисами гиперболы.

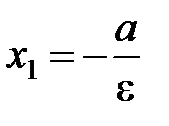– левая директриса, 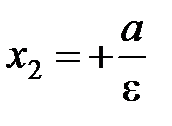– правая директриса.

Директрисы гиперболы обладают тем же свойством, что и директрисы эллипса 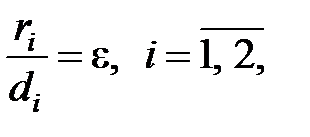(18)

т. е. отношение расстояния 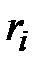от любой точки гиперболы до фокуса к расстоянию 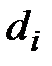от нее до соответствующей директрисы есть величина постоянная, равная эксцентриситету гиперболы.

Для гиперболы важную роль играют также прямые 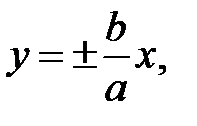(19)

которые являются ее асимптотами, т. е. прямыми к которым график гиперболы неограниченно близко приближается, но не пересекает их. Заметим, что асимптоты гиперболы совпадают с диагоналями прямоугольника (если их продолжить)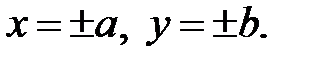

Следует отметить, что если уравнение гиперболы имеет вид (14), т. е. ее фокусы находятся на оси Оу, то изменятся формулы для вычисления фокальных радиусов, эксцентриситета, директрис. Так 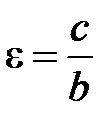– эксцентриситет, 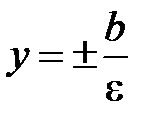– уравнения директрис.