Известно, что общее решение уравнений (2.5) записывается в виде:
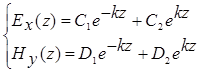 (3.1)
(3.1)
Возбуждение поля происходит сверху, поэтому поле не может неограниченно возрастать с глубиной. Следовательно, 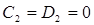 и система (3.1) упрощается:
и система (3.1) упрощается:
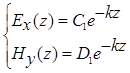 (3.2)
(3.2)
Подставим эти выражения для 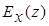 и
и 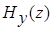 во второе уравнение системы (2.3):
во второе уравнение системы (2.3):
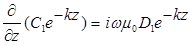
Выполнив дифференцирование, получим:
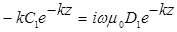
Сократим экспоненты в левой и правой частях и поделим на 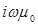 :
:
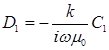
С учетом этого система (3.2) примет вид:
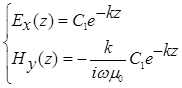
Теперь осталось избавиться от неизвестной константы 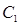 . Для этого введем новую величину - импеданс
. Для этого введем новую величину - импеданс 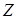 , которую определим как отношение
, которую определим как отношение 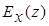 и
и 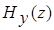 :
:
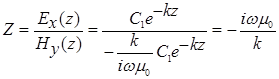 (3.3)
(3.3)
Здесь 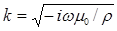 - волновое число полупространства.
- волновое число полупространства.
Таким образом, в любой точке однородного полупространства (в том числе на его поверхности) импеданс принимает одинаковые значения и зависит только от частоты и удельного сопротивления полупространства. Что же касается компонент 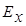 и
и 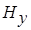 , то они зависят от источника (эта зависимость заключена в константах
, то они зависят от источника (эта зависимость заключена в константах 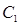 и
и 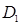 ) и затухают с глубиной. Рассмотрим процесс этого затухания подробнее.
) и затухают с глубиной. Рассмотрим процесс этого затухания подробнее.
Из формул (3.2) следует, что
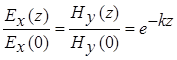
Представляя волновое число 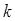 в виде суммы действительной и мнимой частей, мы можем записать полученную экспоненту в виде:
в виде суммы действительной и мнимой частей, мы можем записать полученную экспоненту в виде:
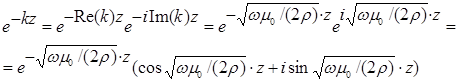
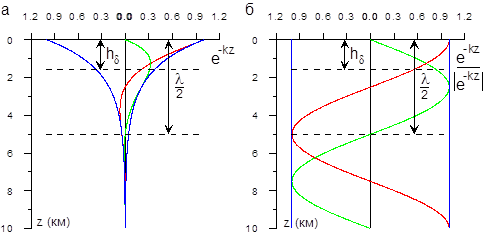 Рис. 3. Изменение
Рис. 3. Изменение 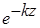 с глубиной. с глубиной.
|
Первый множитель этого произведения отражает затухание с глубиной, а второй - осцилляцию. На рис. 3 (а) показано поведение поля частотой 1 Гц для полупространства с удельным сопротивлением 10 Ом*м. Синей линией показано убывание с глубиной модуля 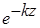 , красной - действительной части
, красной - действительной части 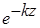 , зеленой - мнимой части
, зеленой - мнимой части 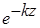 . Из рисунка видно, что эффект затухания существенно превышает эффект осцилляции. На рис. 3 (б) эти величины нормированы на модуль
. Из рисунка видно, что эффект затухания существенно превышает эффект осцилляции. На рис. 3 (б) эти величины нормированы на модуль 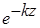 , т.е. эффект затухания исключен, что позволяет более наглядно изучить эффект осцилляции. В частности, в момент времени, когда поле на поверхности максимально, на глубине
, т.е. эффект затухания исключен, что позволяет более наглядно изучить эффект осцилляции. В частности, в момент времени, когда поле на поверхности максимально, на глубине 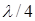 оно еще будет равным нулю, а на глубине
оно еще будет равным нулю, а на глубине 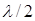 - и вовсе находиться в противофазе и т.д. (см. график действительной части
- и вовсе находиться в противофазе и т.д. (см. график действительной части 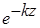 ). Через время, равное четверти периода колебаний, волна распространится на глубину
). Через время, равное четверти периода колебаний, волна распространится на глубину 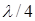 (см. график мнимой части
(см. график мнимой части 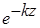 ).
).
Период осцилляции (длину волны 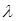 ) найдем из условия:
) найдем из условия: 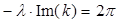 . Расписывая мнимую часть
. Расписывая мнимую часть 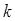 , получим:
, получим: 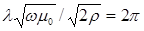 . Отсюда
. Отсюда
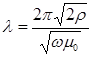
Толщиной скин-слоя 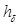 называют глубину, на которой поле затухает в
называют глубину, на которой поле затухает в  раз. Ее можно найти из условия:
раз. Ее можно найти из условия: 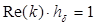 . После преобразований получим:
. После преобразований получим:
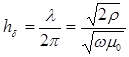
Толщина скин-слоя характеризует глубинность исследований, причем она может использоваться и в горизонтально-слоистой среде. При этом вместо сопротивления полупространства подставляется кажущееся сопротивление на данной частоте.
 2015-06-28
2015-06-28 674
674








