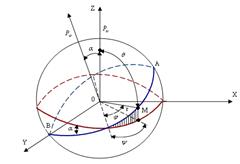
 Рух електрона в просторі і його положення характеризується трьома координатами, і є рухом з трьома степенями вільності. В сферичній системі координат (
Рух електрона в просторі і його положення характеризується трьома координатами, і є рухом з трьома степенями вільності. В сферичній системі координат (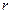 ,
, 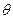 ,
, 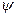 ) відповідно до умов Зоммерфельда ми отримаємо три рівняння, які описуватимуть рух з трьома степенями вільності:
) відповідно до умов Зоммерфельда ми отримаємо три рівняння, які описуватимуть рух з трьома степенями вільності:
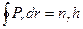
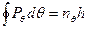
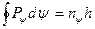 (2.54)
(2.54)
Тут 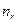 - радіальне квантове число
- радіальне квантове число
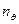 - екваторіальне квантове число
- екваторіальне квантове число
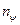 - широтне квантове число
- широтне квантове число
Тут кут 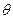 між віссю Z і електроном (в точці М), який рухається по еліптичній орбіті АВ, яка складає кут
між віссю Z і електроном (в точці М), який рухається по еліптичній орбіті АВ, яка складає кут 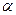 з площиною (XOY).
з площиною (XOY).
Якщо на систему не діють зовнішні сили, то орбіта руху електрона буде нерухомою і плоскою. Визначимо величини інтегралів руху, які входять в рівняння (2.54). Вираз для кінетичної енергії має вигляд (для сферичної системи координат):
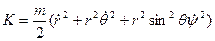 (2.55)
(2.55)
А повна енергія буде як сума кінетичної і потенціальної:
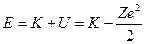 (2.56)
(2.56)
Або через функцію Гамельтона: 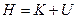
Тоді для величин імпульсів маємо:
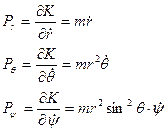 (2.57)
(2.57)
Враховуючи, що без дії зовнішніх сил, повна енергія системи визначається головним квантовим числом, то отримаємо:
n=nr+nθ+nψ=nr+nφ (2.58)
nθ+nψ=nφ
В вираз повної енергії системи координата 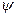 не входить, отже:
не входить, отже:
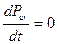 або
або 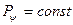
Тоді на основі третьої умови квантування в (2.54) маємо:
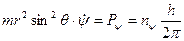 (2.59)
(2.59)
Величина 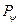 являє собою проекцію повного моменту кількості руху електрона
являє собою проекцію повного моменту кількості руху електрона 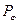 на вісь Z. Позначимо
на вісь Z. Позначимо 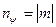 , тоді
, тоді 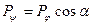 ;
; 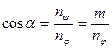
Враховуючи, що 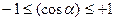 та nθ+nψ=nφ, то значення квантового числа
та nθ+nψ=nφ, то значення квантового числа 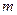 може бути в межах:
може бути в межах:

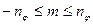 (2.60)
(2.60)
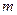 приймає (2 nφ+1) [
приймає (2 nφ+1) [ 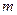 =0;
=0; 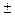 1;
1; 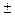 2…
2… 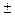
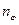 ] значень
] значень
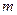 - магнітне квантове число, так як воно визначає проекцію магнітного і механічного моментів на напрямок зовнішнього магнітного поля. Отримаємо ще більш значне виродження системи по
- магнітне квантове число, так як воно визначає проекцію магнітного і механічного моментів на напрямок зовнішнього магнітного поля. Отримаємо ще більш значне виродження системи по 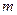 ,(раніше було тільки по
,(раніше було тільки по 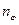 =К, азимутальному).
=К, азимутальному).
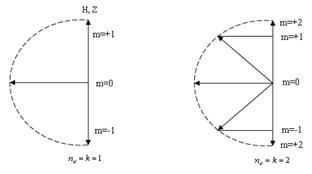
Накладання магнітного поля знімає виродження по 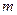 . Орбіти руху електрона з різним значенням
. Орбіти руху електрона з різним значенням 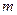 будуть мати в такому випадку різні енергії. Визначимо орієнтації механічного моменту в магнітному полі:
будуть мати в такому випадку різні енергії. Визначимо орієнтації механічного моменту в магнітному полі:
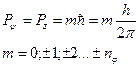
 2015-06-28
2015-06-28 1288
1288








