2015-06-28
702
Задача №1 В аффинной системе координат R=(О,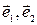 
) дан треугольник АВС координатами своих вершин. Вычислить координаты центра тяжести треугольника (точки пересечения медиан).
Решение
 |
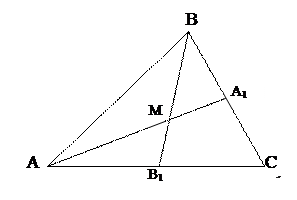Рис.6
Так как точка В1− середина отрезка АС, то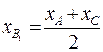 
, 
.
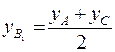2. По свойству медианы │ВМ│:│МВ1│= 2:1. => λМ = 2. Используя соотношения (4), получаем:
.
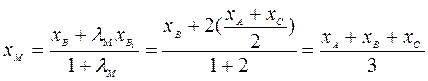Аналогично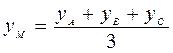 
.
Ответ: М(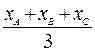
; 
).
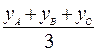Задача №2 Отрезок АВ с концами А(-5;8) и В(-2;0) делится точками C,,E последовательно на равные части. а) В каком отношении точки C,, B делят отрезок LЕ? б) Найти координаты точки Е. в) Определить координаты точек, делящих отрезок в отношении: l1=-2,l2=1/2 и координаты точки М, для которой λМ = (АВ,М) = = ─ 5.Решение
Рис.7
а). Определим отношение, в котором точка С делит отрезок АЕ. По определению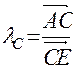 
. Так как 
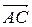и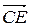 
сонаправлены, то λС > 0 и 
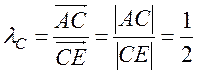. Аналогично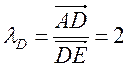 
б). Вычислите самостоятельно координаты точки Е.
