Задача. В аффинной системе координат дан вектор 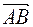 , для которого известны координаты точек начала и конца. Вычислить координаты
, для которого известны координаты точек начала и конца. Вычислить координаты
вектора 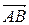 .
.
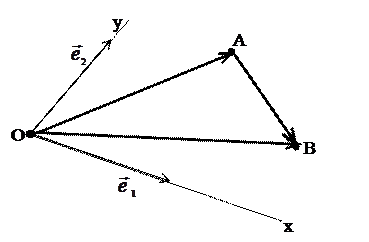 Дано:
Дано:
R=(О, 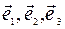 ).
).
А(xL;yL;zL)
B(xB;yB;zB)
Вычислить:
Координаты 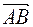
Решение
Введём в рассмотрение радиус−векторы 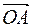 и
и 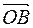 точек А и В. Тогда
точек А и В. Тогда
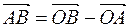 . По определению координат точки
. По определению координат точки 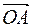 = { xL;yL} и
= { xL;yL} и 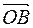 = { xB;yB }. Учитывая следствие из теоремы о координатах разности векторов, получаем:
= { xB;yB }. Учитывая следствие из теоремы о координатах разности векторов, получаем:
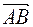 = {xB−xL; yB− yL; zB− zL} = {xB−xL; yB− yL; zB− zL} |
(2)
Вывод: Каждая координата вектора равна разности соответствующих координат конца и начала вектора.
 2015-06-28
2015-06-28 2012
2012
