Пример 1. Рассчитайте относительную молекулярную массу хлорной кислоты НСIO4.
Решение. 1. Используя периодическую систему Д. И. Менделеева или таблицу относительных атомных масс (см. приложение 1), находим значения Ar элементов, входящих в состав хлорной кислоты: Ar(Н) = 1; Ar(С1) = 35,5; Ar(О) = 16.
2. Рассчитываем относительную молекулярную массу хлорной кислоты:
Мr(НСlO4) = Ar(Н) + Ar(С1) + 4 Ar(О);
Mr(НСlО4) = 1 + 35,5 + 4·16 = 100,5.
Пример 2. Определите среднюю массу атома фтора (в кг), если известно, что масса атома углерода- 12 равна 1,993·10-26 кг.
Решение. 1. Рассчитываем массу (в кг) атомной единицы массы:
т (а. е. м.) = 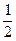 т (12С); т (а. е. м.)=
т (12С); т (а. е. м.)= 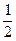 ·1,993·10-26 = 1,66·10-27 кг.
·1,993·10-26 = 1,66·10-27 кг.
2. Зная, что Ar (F) = 19, вычисляем массу атома фтора:
m (F) = Ar (F)· m (а. е. м.); m (F) = 19·1,66·10-27 кг = 3,15·10-26 кг.
Пример 3. Вычислите количество вещества магния в образце массой 2,6 г.
Решение. 1. Относительная атомная масса магния равна 24, следовательно, молярная масса магния равна 24 г/моль, т.е. М(Мg)= 24 г/моль.
2. Вычисляем количество вещества цинка в образце:
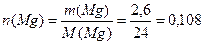 (моль).
(моль).
Пример 4. Вычислите массу иодида натрия NaI, если количество вещества его равно 0,02 моль.
Решение. 1. Рассчитываем относительную молекулярную массу иодида натрия:
Мr (NaI) = Ar (Na) + Аr (I); Мr (NaI) = 23 + 127 = 150.
Молярная масса иодида натрия M (Nа1) =150 г/моль. 5
2. Определяем массу иодида натрия:
m (Nа1) = n (Ма1)· М (Nа1); т (NаI) = 0,02 моль·150 г/моль = 3 г.
Пример 4. Рассчитайте число молекул Вr, в броме массой 6,4 г.
Решение.1. Учитывая, что молярная масса брома М (Вr2) =160 г/моль, вычисляем количество вещества Вr:
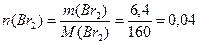 (моль).
(моль).
2. Рассчитываем число молекул (структурных единиц) в веществе:
N (Вr2) = n (Вr2)· NА; N (Вr2) = 0,04 · 6,02·1023 = 2,41·1022.
Пример. Вычислить плотность по водороду газа, 800 мл которого при 627 мм рт. ст. и 39° С имеют массу 0,873 г.
Решение.
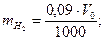
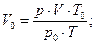
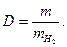
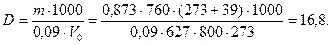
Пример. Вычислить плотность пропана С3Н8 по воздуху. Средний молекулярный вес воздуха Мв = 29.
Решение.
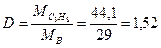
Вычисление плотности и состава газовой cмеси. Этивычисления наиболее просто производятся по правилу смешения. Согласно этому правилу, в двухкомпонентной газовой смеси объемы газов, составляющих смесь, обратно пропорциональны разностям плотностей всей смеси и отдельных ее компонентов.
Правило смешения выражает закономерность количественных отношений компонентов в смеси. Оно применимо только к таким свойствам составных частей, на величину которых не влияет присутствие в смеси других составных частей. Поэтому значение свойства смеси слагается аддитивно, т. е. посредством суммирования значений свойств компонентов, образующих смесь. К таким свойствам относятся плотность, масса, процентная концентрация раствора и др. Для двухкомпонентной смеси правило смешения получает следующее выражение: количества компонентов в смеси обратно пропорциональны разностям свойств компонентов и смеси. Математически - это выводится следующим образом. Обозначим количество одного компонента через А, а количество другого через В. Тогда количество смеси будет А + В. Обозначим свойство первого компонента через х1, второго — через х2, смеси — через х. Составляем уравнение:
x1A + x2B = x(A+B)
Преобразуя, получим:
x1A + xA = XB – x2B,
A(x1 – x) = B(x – x2).
Отсюда
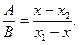
Пример. Газовая смесь состоит из 40 объемных процентов азота и 60 объемных процентов кислорода. Вычислить плотность смеси по водороду.
Решение. Обозначим искомую плотность смеси по водороду через Dх. Плотность азота по водороду 14. Плотность кислорода по водороду 16.
Используя для решения правило смешения, составляем пропорцию:
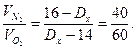
Решая пропорцию, находим:
960 - 60 Dx = 40 Dx - 560;
100 Dx = 1520;
Dх = 15,2.
Пример. Плотность по водороду газовой смеси, состоящей из метана СН4 и кислорода, равна 14. Вычислить объемный состав этой смеси.
Решение. Так как плотность по водороду метана равна 8, а кислорода 16, то, согласно правилу смешения,
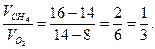
Деля 100% пропорционально этому отношению, находим:
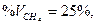
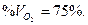
Зависимость между количествами компонентов двухкомпонентной системы, вытекающая из правила смешения, часто выражается в форме так называемой «диагональной схемы», которая строится следующим образом. В точке пересечения двух отрезков прямой обозначают свойство смеси. У концов обоих отрезков, расположенных по одну сторону от пересечения, обозначают свойства компонентов смеси. У других концов каждого из отрезков обозначают разности свойств смеси и компонентов ее. Количества компонентов относятся как числа, расположенные на одной горизонтальной линии, со свойством соответствующего компонента.
Согласно этому схема для выражения состава вышеуказанной смеси метана и кислорода получила бы следующее выражение:
 8 2
8 2
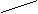 14
14
16 6
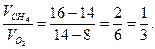
Пример 3. Вычислить объемное содержание водорода и оксида углерода(IV) в смеси газов, имеющей плотность по водороду 12,2 и содержащей, кроме водорода и оксида углерода(IV), 45% азота.
Решение. В тех случаях, когда смесь содержит более двух компонентов, для расчета требуется знать содержание в смеси остальных компонентов. Из условия задачи следует, что водород и оксида углерода(IV) составляют 55% от объема всей смеси. Используя его и опираясь на правило смешения, вычисляем плотность водорода и оксида углерода(IV) в смеси, рассматривая всю смесь как двухкомпонентную систему, в которой одним компонентом является смесь водорода и СО2, а другим — азот.
Обозначим общую плотность водорода и оксида углерода(IV) в смеси через D(H2+CO2), соответственно плотность азота — через DN2, а плотность смеси — через D. Находим: 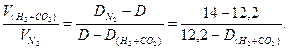
Согласно условию,
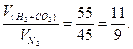
Поэтому
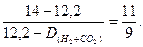

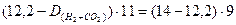 .
.
Решая это уравнение, находим:
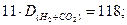
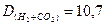
Вычислив плотность смеси Н2 и СО2, находим, как относятся друг к другу объемы водорода и оксида углерода(IV) в смеси. Так как DH2 = 1, DCO2 = 22, а плотность их смеси 10,7, то
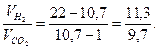
Чтобы выразить содержание водорода и двуокиси углерода в процентах по отношению к объему всей смеси, делим 55% пропорционально числам найденного отношения; получаем: 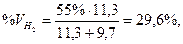
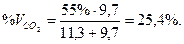
Вычисление молекулярного веса газа по его плотности. Молекулярный вес какого-либо газа равен произведению относительной его плотности по другому газу на молекулярный вес этого другого газа.
Пример 4. Плотность газа по воздухе 1,45. Вычислить молекулярный вес газа.
Решение.
М = 1,45·29=42 ( г/моль ).
Пример 1. При окислении 2,81 г кадмия получено 3,21 г окcида кадмия. Вычислить эквивалент кадмия.
Решение. По массе кадмия и массе его оксиде находим массу кислорода:
mO = 3,21 – 2,81 = 0,4 (г).
Вводя массу кислорода и массу кадмия в пропорцию, выражающую закон эквивалентов, получаем:
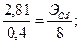


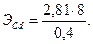
Пример 2. Для реакции между магнием и кислотой взято 0,183 г магния; получено 182,7 мл водорода при 20° С и 750 мм рт. ст. Вычислить эквивалент магния.
Решение. Расчет можно произвести двумя методами.
Первый метод: по уравнению Клапейрона — Менделеева вычисляем массу водорода, исходя из его объема
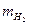 =
= 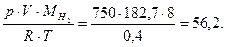
Затем производим расчет как в предыдущем примере:
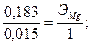
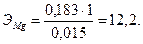
Второй метод: объем водорода приводим к нормальным условиям
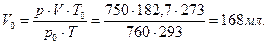
В пропорции, выражающей закон эквивалентов, заменяем массу водорода его объемом при нормальных условиях, а эквивалент водорода — его грамм-эквивалентным объемом, который вычисляется следующим образом. Грамм-эквивалент водорода (1 г) в 2 раза меньше моля водорода (2 г). Соответственно грамм-эквивалентный объем водорода в 2 раза меньше мольного объема. Так как мольный объем любого газа при нормальных условиях равен 22 400 мл, то грамм-эквивалентный объем водорода при этих условиях равен 11200 мл.
Вводя конкретные значения величин в пропорцию, выражающую закон эквивалентов, находим:
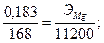
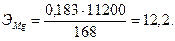
Пример 3. Вычислить эквивалент железа исходя из того, что в реакции соединения с серой на 0,85 г его приходятся 0,50 г серы, эквивалент которой равен 16.
Решение. Вводя значение эквивалента серы в пропорцию, находим:
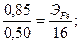
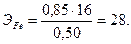
Пример 4. Вычислить валентность хрома в оксиде, имеющем состав: Сr 68,42%, О 31,58%.
Решение. Находим эквивалент хрома обычным путем:
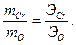
Отсюда
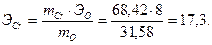
Сравнивая числовое значение эквивалента с атомным весом хрома, находим:
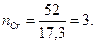
Пример 5. Вычислить эквиваленты Н2SO4 в реакциях обмена, в результате которых образуются: а) кислые соли МеНSО4; б) нормальные соли Ме2SО4 (Ме — одновалентный металл).
Решение. В первом случае в реакции участвует от "каждой молекулы кислоты один ион водорода, а во втором случае - два. Поэтому в первом случае эквивалент Н2SО4 численно равен молекулярной массе, т. е. 98. Во втором случае эквивалент Н2SO4 численно равен половине молекулярной массы, т. е. 49.
Пример 6. Вычислить эквивалент А12(SО4)3 при взаимодействии с NаОН.
Решение. Реакция протекает по уравнению:
Аl2(SО4)3 + 6NаОН →3Nа2SО4 + 2 Аl(ОН)3.
В реакции от каждой молекулы Аl2(SО4)3 участвуют два атома алюминия, валентность которого 3. Отсюда
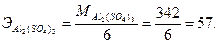
Пример 7. Вычислить эквивалент КА1(SO4)2 при взаимодействии с КОН.
Решение. Реакция протекает по уравнению:
КАl(SO4)2 + 3КОН → Аl(ОН)3 + 2K2SО4
От КАl(SO4)2 в обмене участвует один только алюминий. Поэтому эквивалент КАl(SO4)2 численно равен частному от деления молекулярного веса на 3:
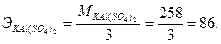
Пример 8. Вычислить эквивалент КАl(SO4)2 при взаимодействии с ВаС12.
Решение. Реакция протекает по уравнению:
КАl(SO4)2+ 2ВаС12→ АlCl3 + KCl + 2BaSО4.
Из уравнения реакции видно, что оба металла К и А1 из КАl(SO4)2 обмениваются на металл Ва из ВаС12. Так как валентность калия равна 1, а валентность алюминия 3, то эквивалент КАl(SO4)2 в данном случае численно равен молекулярному весу КАl(SO4)2, деленному на 4:
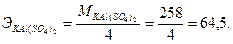
Пример 9. На нейтрализацию 0,336 г кислоты расходуется 0,292 г NаОН. Вычислить эквивалент кислоты.
Решение. Рассмотренным ранее методом находим ЭNaOH = 40. Согласно закону эквивалентов,
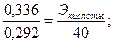
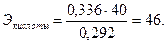
Пример. Найти простейшую формулу оксида хрома, содержащего 68,4% (масс.) хрома.
Решение. Обозначим числа атомов хрома и кислорода в простейшей формуле оксида соответственно через х и у. Атомные массы этих элементов равны 52 и 16. Поэтому массы хрома и кислорода в составе оксида относятся как 52 x: 16 у. По условиям задачи это отношение равно 68,4: 31,6. Следовательно,
52 x: 16 y = 68,4: 31,6, откуда х: у = 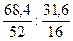 = 1,32: 1,98.
= 1,32: 1,98.
Чтобы выразить полученное отношение целыми числами, разделим оба его члена на меньший из них: х:у = 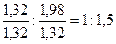 ,
,
а затем умножим оба члена последнего отношения на два:
х:у= 2:3.
Таким образом, простейшая формула оксида хрома Сr2О3.
Пример. При полном сжигании 2,66 г некоторого вещества получилось 1,54 г СО2 и 4,48 г SО2. Найти простейшую формулу вещества.
Решение. Состав продуктов горения показывает, что вещество содержало углерод и серу. Кроме этих двух элементов в состав его мог входить и кислород.
Массу углерода, входившего в состав вещества, находим по массе образовавшегося СO2. Мольная масса СО2 равна 44 г/моль; при этом в 1 моле СO2 содержится 12 г углерода. Находим массу углерода т, содержащуюся в 1,54 г СО2:
44: 12 = 1,54: m; m = 12·1,54/44 = 0,42 г.
Вычисляя аналогичным способом массу серы, содержащуюся в 4,48 г SО2, получаем 2,24 г.
Таким образом, в сгоревшем веществе на 0,42 г углерода приходится 2,24 г серы. Так как сумма этих двух масс равна общей массе сгоревшего вещества (2,66 г), то кислорода в нем не содержится.
Вычисляем отношение числа атомов углерода (х) и серы (у) в молекуле сгоревшего вещества: 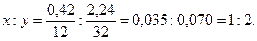
Следовательно, простейшая формула вещества СS2.
Пример. Газообразное соединение азота с водородом содержит 12,5% (масс.) водорода. Плотность соединения по водороду равна 16. Найти молекулярную формулу соединения.
Решение. Находим отношение числа атомов азота (х) к числу атомов водорода (у) в молекуле соединения:
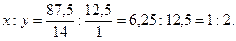
Простейшая формула соединения NH2. Этой формуле отвечает молекулярная масса, равная 16. Истинную молекулярную массу вещества находим, исходя из его плотности по водороду:
М = 2 · 16 = 32.
Таким образом, истинная молекулярная масса вещества вдвое больше вычисленной по его простейшей формуле. Следовательно, молекулярная формула соединения N2H4.
Пример. Анализ уксусной кислоты показывает, что в ней на 2,1 вес. ч. углерода приходится 0,35 вес. ч. водорода и 2,8 вес. ч. кислорода. Плотность паров уксусной кислоты по водороду равна 30. Выведите истинную формулу уксусной кислоты.
Решение. 1. Находим молекулярный вес уксусной кислоты по формуле:
М = 2·DH2 = 2·30 = 60.
2. Запишем формулу С x Н y О z, находим отношение между числами:
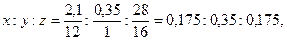
выразим это отношение целыми числами, т. е. разделим на 0,175. Тогда х: у: z = 1: 2: 1. Следовательно, простейшая формула уксусной кислоты СН2О. Согласно этой формуле молекулярный вес вещества равен 30, а должен быть 60 г/моль.
Пример. К раствору 0,404 г хлорида меди прилили избыток раствора АgNO3. Образовался осадок АgС1 массой 0,86 г. Вычислить количественный состав хлорида меди.
Решение. По массе и составу АgС1 вычисляем массу хлора в хлориде меди:
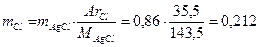 (г).
(г).
о массе хлорида меди и массе хлора вычисляем массу меди:
тСи = mCuCl2 - mCl = 0,404 - 0,212 = 0,192 (г).
Отсюда
mCu : mCl = 0,192: 0,212 = 48: 53.
Пример. Найти отношение масс NаОН и А1(ОН)3 в реакции, протекающей по уравнению:
А12(SO4)3 + 6NаОН = 2А1(ОН)3 + 3Nа2SО4
Решение.
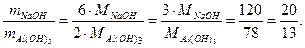
Пример. Найти отношение объема этана С2Н6 к объему кислорода в реакции, протекающей по уравнению:
2С2Н6 + 7O2 = 4СО2 + 6Н2О.
Решение.V С2Н6: VО2 = 2 V мол: 7 V мол.
Так как мольные объемы газов при одинаковых условиях равны друг другу, то
V С2Н6: VО2 = 2: 7.
Отсюда общий вывод: объемы участвующих в реакции газов относятся друг к другу как коэффициенты в уравнении реакции.
Пример. Найти отношение массы КС1O3 к объему О2 в реакции, протекающей по уравнению:
2КС1O3 = 2КС1 + 3О2
Решение.
m КС1O3: V O2 = 2MКС1O3: 3Vмол.
Подставляя числовые значения величин в пропорцию, получаем:
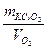 =
= 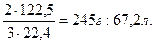
Пример. Смесь солей NaС1 и КС1, масса которой 0,325 г, растворили в воде. К приготовленному раствору прибавили раствор АgNО3 в избытке. Выпал осадок АgС1, масса которого 0,717 г. Сколько NaCl и сколько КС1 содержалось в смеси?
Решение. Алгебраический метод решения.
По уравнениям реакций
NaCl + АgNO3 = АgС1 + NаNО3
КС1 + АgNO3 = АgС1 + КNO3
определяем, сколько АgС1 получается из 1 г каждого компонента смеси:
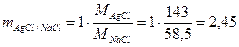 (г),
(г),
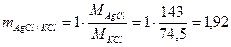 (г).
(г).
Обозначим массу NаС1 через х и массу КС1 — через у. Тогда масса АgС1, получаемого в результате реакции с NаС1, будет 2,45 х, а масса АgС1, получаемого в результате реакции с КС1, будет 1,92 у. Составляем систему из двух
 уравнений:
уравнений:
 x + y = 0,325
x + y = 0,325
2,45 x + 1,92 y = 0,717
и решаем ее следующим образом: умножаем все члены 1-го уравнения на коэффициент при х во 2-м уравнении и вычитаем 2-е уравнение из 1-го:
2,45 x + 2,45 y = 0,325·2,45 = 0,796
2,45 х + 1,92 y = 0,717
0,53у = 0,079
Отсюда
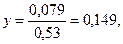
х = 0,325 - 0,149 = 0,176.
Состав смеси: т NaCl = 0,176 г; m KCl = 0,149 г.
Арифметический метод решения.
Вычисления начинаются так же, как и при алгебраическом методе: с нахождения массы АgС1, соответствующей 1 г NаС1 и 1 г КС1.
Сличая эти массы, видим:
m АgС1/NaС1 больше m AgCl/KCl, на 2,45 г -1,92 г = 0,53 г.
Вычисляем, какой была бы масса АgС1, если бы вместо смеси был один только NaC1 такой же массы, как вся смесь:
m АgCl = 2,45 · 0,325 = 0,796 г.
Эта масса больше массы фактически полученного АgС1 на
0,796 г - 0,717 г = 0,079 г.
Разница получилась вследствие замены содержавшегося в смеси КС1 на NaС1; а так как разница в массе АgС1, получаемого из 1 г NaС1, сравнительно с массой АgС1, получаемого из 1 г КС1, равна 0,53 г, то, деля 0,079 на 0,53, находим, сколько КС1 содержалось в смеси:
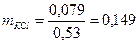 г.
г.
Количество NaC1 находим по разности массы смеси и массы КС1:
m NаС1 = 0,325 г - 0,149 г = 0,176 г,
Решение по правилу смешения.
Начало вычислений такое же, как и в других методах. Затем вычисляем, сколько АgС1 приходится на 1 г смеси согласно условию задачи:
m AgCl (на единицу массы) = 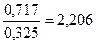 г.
г.
Далее составляем пропорцию по правилу смешения аналогично тому, как это показано для газовых смесей:
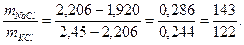
Деля массу смеси пропорционально отношению 143:122, получим:
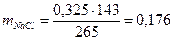 г.
г.
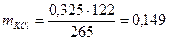 г.
г.
 2015-06-28
2015-06-28 9228
9228
