Каждая плоскость в пространстве Oxyz определяется линейным алгебраическим уравнением первой степени.
Способы задания и уравнения плоскости:
1) точка М0(x0; y0; z0) принадлежит плоскости, вектор 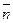 (А; В; С) перпендикулярен плоскости, тогда уравнение плоскости имеет вид: А(x – x0) + B(y – y0) + C(z – z0) = 0;
(А; В; С) перпендикулярен плоскости, тогда уравнение плоскости имеет вид: А(x – x0) + B(y – y0) + C(z – z0) = 0;
2) уравнение плоскости в отрезках: 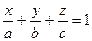 , где а, в, с – абсцисса, ордината, аппликата точек пересечения плоскости с координатными осями Ox, Oy, Oz соответственно;
, где а, в, с – абсцисса, ордината, аппликата точек пересечения плоскости с координатными осями Ox, Oy, Oz соответственно;
3) точка М0(x0; y0; z0) принадлежит плоскости, вектора 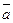 (а1; а2; а3) и
(а1; а2; а3) и 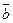 (b1; b2; b3) параллельны плоскости, тогда уравнение плоскости имеет вид:
(b1; b2; b3) параллельны плоскости, тогда уравнение плоскости имеет вид: 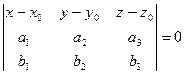 ;
;
4) уравнение плоскости, проходящей через три точки М1(x1; y1; z1), M2(x2; y2; z2), M3(x3; y3; z3): 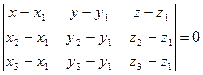 ;
;
5) нормальное уравнение плоскости: x cos 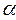 + y cos
+ y cos 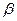 + z cos
+ z cos 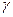 -
- 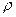 = 0, где
= 0, где 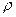 - длина перпендикуляра, опущенного из начала координат на плоскость,
- длина перпендикуляра, опущенного из начала координат на плоскость, 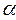 ,
, 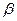 ,
, 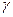 - углы, образованные перпендикуляром с координатными осями, причём
- углы, образованные перпендикуляром с координатными осями, причём 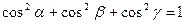 .
.
Ax + By + Cz + D = 0 – общее уравнение плоскости, координаты нормального вектора (А; В; С).
Общее уравнение плоскости приводится к нормальному виду путём умножения на нормирующий множитель 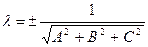 , знак которого противоположен знаку свободного слагаемого в общем уравнении плоскости.
, знак которого противоположен знаку свободного слагаемого в общем уравнении плоскости.
Уравнение пучка плоскостей, проходящих через прямую, образованную пересечением двух плоскостей A1x + B1y + C1z + D1 = 0 и A2x + B2y + C2z + D2 = 0 имеет вид A1x + B1y + C1z + D1 + 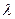 (A2x + B2y + C2z + D2) = 0.
(A2x + B2y + C2z + D2) = 0.
Уравнение связки (пучка) плоскостей A(x – x0) + B(y – y0) + C(z – z0) = 0.
Угол между двумя плоскостями A1x + B1y + C1z + D1 = 0 и A2x + B2y + C2z + D2 = 0 вычисляется по формуле 
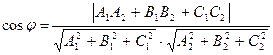 .
.
Взаимное расположение двух плоскостей:
1) 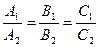 - плоскости параллельны;
- плоскости параллельны;
2) А1А2 + В1В2 + С1С2 = 0 – плоскости перпендикулярны;
3) 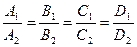 - плоскости совпадают;
- плоскости совпадают;
4) 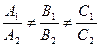 - плоскости пересекаются.
- плоскости пересекаются.
Расстояние от точки М0(x0; y0; z0) до плоскости Ax + By + Cz + D = 0 находится по формуле d = 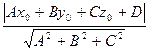 .
.
 2015-06-28
2015-06-28 657
657








