Плоскость и прямая в пространстве
Определение. Уравнение вида
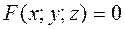 (2)
(2)
называется уравнением поверхности 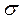 , если любая точка поверхности
, если любая точка поверхности 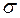 имеет координаты, удовлетворяющие уравнению (2). Любая точка, не лежащая на поверхности
имеет координаты, удовлетворяющие уравнению (2). Любая точка, не лежащая на поверхности 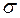 , имеет координаты, не удовлетворяющие уравнению (2).
, имеет координаты, не удовлетворяющие уравнению (2).
Пример: 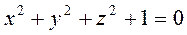
Определение. Многочленом (полиномом) в степени n от трех неизвестных называется сумма, каждое слагаемое которой представляет собой произведение вида 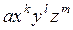 , где
, где 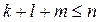 , причем имеется хотя бы одно слагаемое в этой сумме, для которого
, причем имеется хотя бы одно слагаемое в этой сумме, для которого 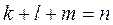 .
.
Во всех определениях 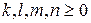 - целые числа.
- целые числа.
Определение. Уравнение (2) называется алгебраическим уравнением степени n, если в этом уравнении функция 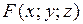 является полиномом степени n от трех неизвестных.
является полиномом степени n от трех неизвестных.
Определение. Поверхность 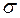 , описываемая алгебраическим уравнением степени n, называется алгебраической поверхностью n-го порядка.
, описываемая алгебраическим уравнением степени n, называется алгебраической поверхностью n-го порядка.
Пример:
1. 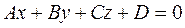
2. 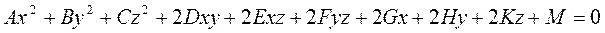
 2015-06-28
2015-06-28 1975
1975
