Лекция №10
Прямая линия на плоскости может быть задана:
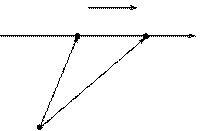
1. Векторным уравнением в параметрической форме.
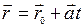 ,
, 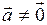 , (1)
, (1)
где 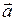 - направляющий вектор прямой,
- направляющий вектор прямой, 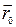 - радиус-вектор фиксированной точки на прямой.
- радиус-вектор фиксированной точки на прямой.
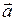
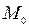
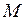
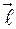
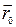
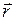
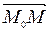
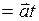 , точка
, точка 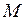 - текущая точка прямой
- текущая точка прямой 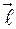 .
.
2. Нормальным векторным уравнением
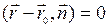 ,
, 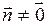 , (2)
, (2)
где 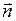 - нормальный вектор прямой.
- нормальный вектор прямой.
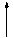
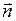
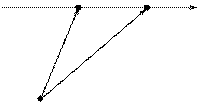
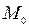
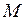
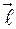
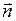
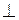
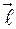
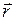
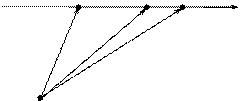
3. Уравнение прямой, проходящей через две различные точки, может быть записано в векторной форме.
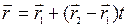 . (3)
. (3)
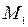
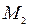
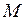
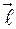
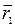
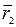
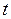 - параметр,
- параметр, 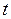
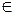 R.
R.
Когда 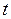 пробегает от
пробегает от 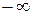 до
до 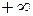 , тогда точка М пробегает всю прямую
, тогда точка М пробегает всю прямую 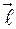 .
.
4. Общее уравнение прямой на плоскости. Уравнение вида
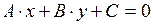 (4)
(4)
называется общим уравнением прямой.
5. Уравнение
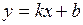 (5)
(5)
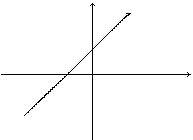
называется уравнением прямой с угловым коэффициентом.
 y
y 
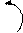 b α
b α
x
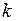 =tgα – угловой коэффициент.
=tgα – угловой коэффициент.
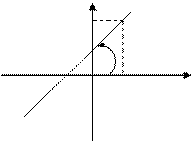
6. Уравнение прямой, проходящей через данную точку в данном направлении.
 y
y 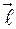

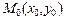
α
0 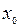 x
x
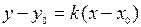 , (6)
, (6)
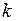 =tgα.
=tgα.
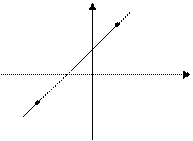
7. Уравнение прямой, проходящей через две данные точки.
 y
y
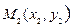
x
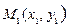
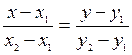 . (7)
. (7)
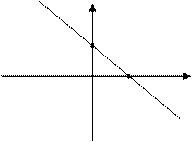
8. Уравнение прямой в отрезках на осях.
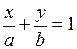 . (8)
. (8)
 y
y

x
0 
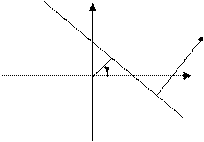
9. Нормальное уравнение прямой линии на плоскости. Расстояние от точки до прямой на плоскости.
 y
y
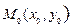
p α x
0 d
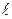
Нормаль к прямой образует угол α с положительным направлением оси 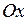 .
.
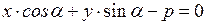 . (9)
. (9)
Расстояние от точки до прямой на плоскости находится по формуле:
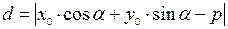 . (10)
. (10)
Для нормального уравнения (9) характерно, что
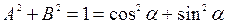 .
.
Чтобы привести общее уравнение прямой к нормальному виду надо обе части этого уравнения умножить на нормирующий множитель 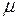 :
:
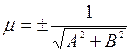 . (11)
. (11)
Знак нормирующего множителя выбирается противоположным знаку свободного члена С в общем уравнении прямой.
10. Параметрические уравнения прямой на плоскости.


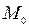
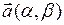
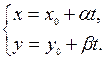
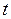 – параметр,
– параметр, 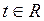 .
.
Пусть две прямые заданы уравнениями:
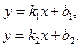
 |
(2) (1)
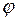
|
Тангенс угла между этими прямыми находится по формуле
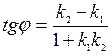 . (12)
. (12)
Признаком параллельности двух прямых является равенство их угловых коэффициентов
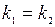 . (13)
. (13)
Признаком перпендикулярности двух прямых является соотношение
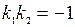 (14)
(14)
или 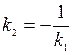 .
.
Угловые коэффициенты взаимно перпендикулярных прямых обратны по величине и противоположны по знаку.
 2015-06-28
2015-06-28 607
607







