2015-06-28
1772
1). Даны вершины треугольника А(8;4), В(-12;-6), С(-4;-12). Составить следующие уравнения:
а) трех его сторон;
б) медианы, проведенной из вершины В;
в) биссектрисы угла С;
г) высоты, опущенной из вершины А на сторону ВС.
2). Начало координат перенесено в точку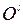 
с координатами (-1;2), оси координат повернуты на угол 
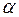, равный 
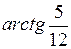. Координаты точек 
, 
, 
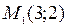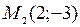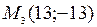определены в новой системе. Вычислить координаты этих точек в старой системе координат.
3). Составить уравнения прямых, параллельных прямой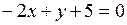 
и отстоящих от точки А(1;-2) на расстоянии 
.
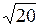4). Даны последовательные вершины выпуклого четырехугольника А(-3;1), В(3;9), С(7;6), D(-2;-6). Определить точку пересечения его диагоналей.
5). Даны вершины треугольника А(1;-2), В(5;4), С(-2;0). Составить уравнения биссектрис его внутреннего и внешнего углов при вершине А.
6). В параллелограмме 
точка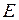 
лежит на диагонали 
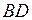, причем 
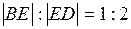. Найти координаты точки плоскости в системе координат 
, 
, 
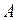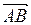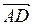, если известны ее координаты 
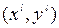в системе координат , 
, 
.
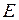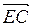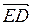Вопросы для самостоятельного изучения
1. Вывод уравнения прямой, проходящей через две данные точки.
|
|
|
2. Вывод нормального уравнения прямой линии на плоскости.
