Блок теоретических материалов «Угол между прямыми на плоскости»
Пусть 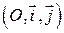 – прямоугольная система координат и даны две прямые
– прямоугольная система координат и даны две прямые 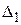 и
и 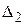 , в некоторой системе координат их можно задать уравнениями
, в некоторой системе координат их можно задать уравнениями 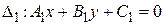 с нормальным вектором
с нормальным вектором 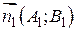 и
и 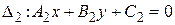 с нормальным вектором
с нормальным вектором 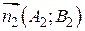 .
.
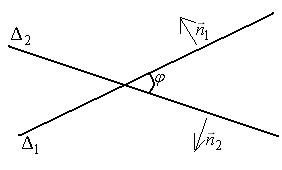
Угол между 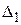 и
и 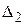 либо равен углу между
либо равен углу между 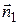 и
и 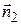 , либо
, либо 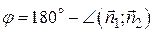 .
.
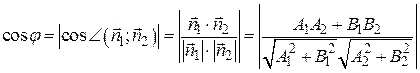
Т.е. имеем
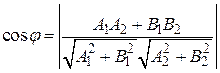 . (5.1)
. (5.1)
Пример5.1. Найти угол между прямыми 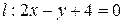 и
и 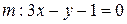 .
.
Решение. Косинус угла между прямыми 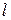 и
и 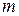 определим по формуле (5.1):
определим по формуле (5.1):
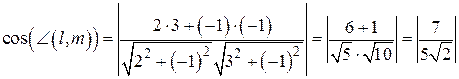 .
.
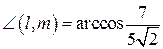 .
.
Ответ: 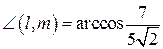 .
.
Если прямые на плоскости заданы в виде 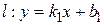 и
и 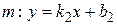 , где
, где 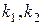 угловые коэффициенты прямых
угловые коэффициенты прямых 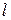 и
и 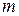 , то искомый угол можно найти по формуле:
, то искомый угол можно найти по формуле:
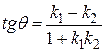 . (5.2)
. (5.2)
Пример 5.2. Найти угол между прямыми 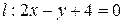 и
и 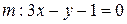 .
.
Решение. Перепишем уравнения прямых в виде: 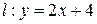 и
и 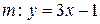 . Тогда по формуле (5.2) имеем:
. Тогда по формуле (5.2) имеем:
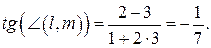
Тогда, 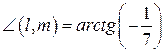 .
.
Ответ: 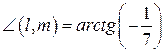 .
.
 2015-06-28
2015-06-28 254
254







