I. Пусть прямые заданы общими уравнениями в ПДСК:
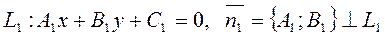
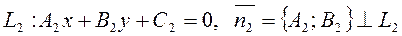
1) прямые 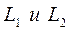 могут быть расположены друг относительно друга следующим образом:
могут быть расположены друг относительно друга следующим образом:
- быть параллельными
- совпадать
- пересекаться
1. 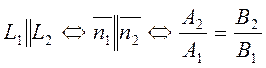 (11)
(11)
(11)- условия параллельности двух прямых.
2. 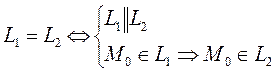
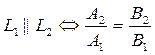
Пусть 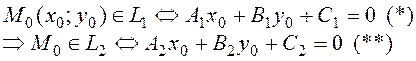
Из (11) 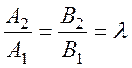
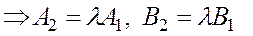
Умножим (*) на 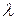 :
:
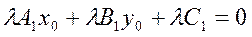 (*’)
(*’)
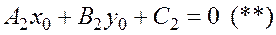
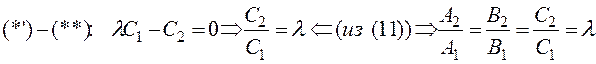 (12) – условие совпадения 2-х прямых.
(12) – условие совпадения 2-х прямых.
3. 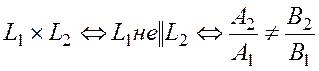 (11) не выполняется (13)
(11) не выполняется (13)
1) Найти точку пересечения прямых.
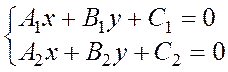
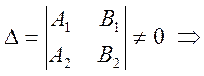 система имеет единственное решение.
система имеет единственное решение.
2) Найти угол между двумя прямыми.
Угол между двумя прямыми равен углу между их нормальными векторами:
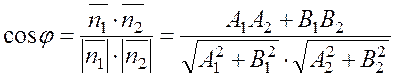 (14)
(14)
II. Пусть прямые заданы каноническими уравнениями
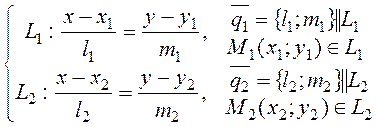
1. 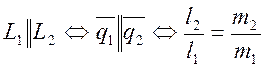 (15)
(15)
2. 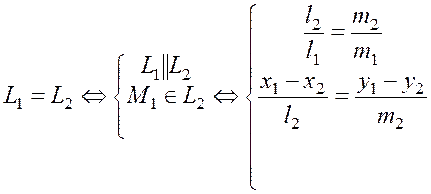 (16)
(16)
3. 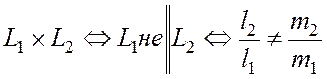 (17)
(17)
Общая точка находится путем совместного решения системы уравнений для 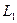 и для
и для 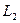 . Угол между двумя прямыми равен углу между их направляющими векторами:
. Угол между двумя прямыми равен углу между их направляющими векторами:
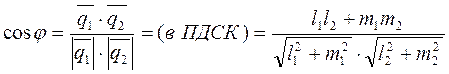 (18)
(18)
III. Пусть прямые заданы уравнениями с угловыми коэффициентами
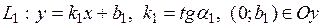
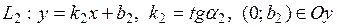
1) 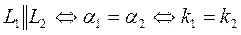 (19)
(19)

2) 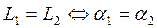 ,
, 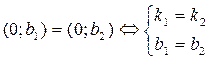 (20)
(20)
Виды уравнения должны быть абсолютно одинаковыми.
3) 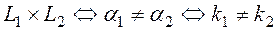 (21)
(21)

Угол φ определяется: от первой прямой до второй против часовой стрелки.
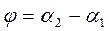
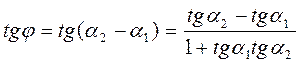
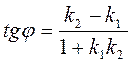 (22)
(22)
 2015-06-28
2015-06-28 1148
1148








