Вещественная форма ряда Фурье

Введение

Данная работа является первой в цикле лабораторных работ в учебной лаборатории «Методов обработки и передачи информации» (МОПИ) физического факультета СПбГУ. Лаборатория выполняется на втором курсе и поддерживает курс лекций "Физические основы методов обработки и передачи информации". К этому времени курс уже прослушан студентами, лаборатория предназначена для закрепления и расширения знаний в этой области.

Представление о спектре сигнала необходимо для разработки устройств передачи информации, оно находит применение для косвенного измерения других физических величин, и просто расчёта электрической цепи. Знание спектра сигнала позволяет лучше понять его природу и не случайно цикл лабораторных работ начинается именно с этой работы.

Работа будет иметь и расчетный, и экспериментальный характер. Экспериментальная часть работы содержит важный инновационный элемент – применение цифровой обработки сигнала, оцифрованного с помощью системы сбора данных. Кроме того, вся расчетная часть работы, а также обработка результатов экспериментов выполняется на базе современного математического пакета МАТЛАБ и его дополнительной библиотеки – Signal Processing Toolbox. Используются заложенные в них возможности математического моделирования разнообразных типов сигналов, обработки данных.

Предполагается, что читатель знаком с основными приемами работы в этом пакете. Программы расчетов и различные дополнения будут отнесены в Приложения к работе.

Вещественная форма ряда Фурье

Рассмотрим периодическую функцию 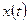с периодом, равным 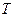: 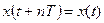, где 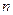– любое целое число. При выполнении определенных условий эта функция может быть представлена в виде суммы, конечной или бесконечной, гармонических функций вида 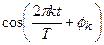, период которых совпадает с периодом исходной функции 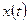, где 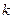– целое число, 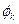– константа. Линейная комбинация таких функций 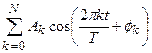, называемая тригонометрическим полиномом N -го порядка, также будет иметь период, равный 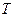. Таким образом, мы будем решать задачу о разложении периодической функции в тригонометрический ряд:

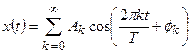(1)

Отдельное слагаемое этой суммы 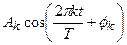называется k -ой гармоникой функции 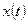. Наша задача заключается в том, чтобы подобрать такие коэффициенты 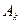и 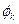, при которых ряд (1) будет сходиться к заданной функции .

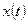Слагаемые в (1) можно записать в другом виде, раскрыв косинус суммы:

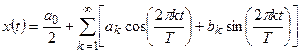(2)

где новые коэффициенты выражаются как 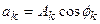, 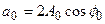и 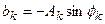. Формула (2) называется вещественной формой тригонометрического ряда. Коэффициенты разложения в тригонометрический ряд Фурье:

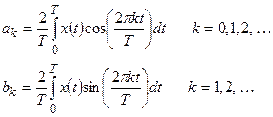(3)

Можно доказать, что тригонометрический ряд будет сходиться равномерно к функции 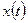, если сходятся ряды 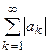и 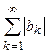. Это будет выполнено, если исходная функция 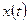удовлетворяет условиям Дирихле:

- функция имеет конечное число разрывов первого рода на периоде,

- на периоде можно выделить конечное число отрезков, на которых функция изменяется монотонно.

Заметим, что для любых периодических электрических сигналов условие Дирихле выполняется. В точках разрыва ряд Фурье сходится к полусумме значений функции слева и справа от точки разрыва. В силу равномерной сходимости ряда каждый следующий его член вносит всё меньший вклад в сумму, поэтому функция 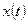может быть приближена с определённой точностью тригонометрическим полиномом порядка N, то есть конечным числом слагаемых.