Спектр дискретного сигнала

Особое внимание стоит уделить дискретным сигналам, так как именно такие сигналы используются в цифровой обработке. Дискретный сигнал в отличие от непрерывного является последовательностью чисел, соответствующих значениям непрерывного сигнала в определённые моменты времени. Условно дискретный сигнал можно рассматривать как непрерывный сигнал, который в определённые моменты времени принимает какие-то значения, а в остальное время равен нулю. Таким образом, например, дискретный 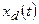сигнал может быть задан как произведение непрерывного сигнала 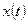на последовательность периодически повторяющихся прямоугольных импульсов 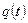– тактирующих импульсов (рис.1).

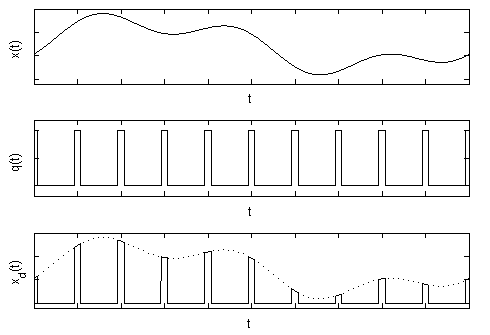
Рис. 1. Дискретизация сигнала.

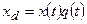(22)

Прямоугольные импульсы имеют длительность 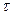, период повторения :

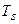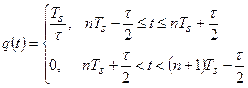(23)

Амплитуда импульса выбрана таким образом, чтобы интеграл импульса по периоду равнялся 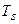. При этом тактирующие импульсы безразмерны. Разложим последовательность таких импульсов в тригонометрический ряд:

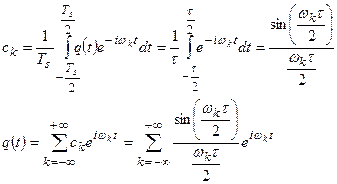(24)

Чтобы получить мгновенные отсчёты сигнала 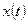, надо устремить длительность импульсов к нулю: 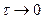. Такой тактирующий сигнал назовём идеальным. При этом коэффициенты разложения 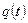в ряд Фурье все будут равны 1.

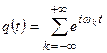(25)

Точно такой же вид имеет разложение в ряд Фурье функции:

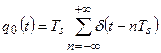(26)

Коэффициенты разложения в тригонометрический ряд тактирующего сигнала :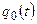

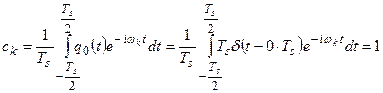(27)

Тогда дискретный сигнал будет иметь вид:

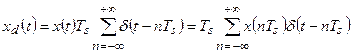(28)

При вычислении преобразования Фурье дискретного сигнала меняем местами операцию суммировании и интегрирования, а потом используем свойство δ -функции:

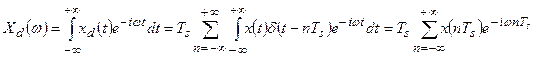(29)

Спектр дискретного сигнала является периодической функцией. Рассмотрим экспоненту в отельном слагаемом 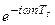как функцию частоты. Её период повторения равен 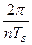. Самый большой период повторения у слагаемых с номерами 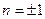, и это, соответственно, будет периодом повторения всего спектра. То есть спектр дискретного сигнала имеет период повторения, равный частоте квантования .

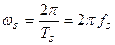Получим ещё одно представление 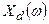. В силу того, что 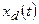является произведением функци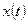й и 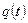, спектр дискретного сигнала 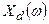вычисляется как свёртка спектров непрерывного сигнала 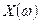и спектра тактирующего сигнала .

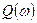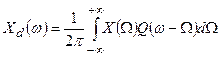(30)

Вычислим 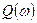, используя (25). Так как 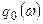периодическая функция, её спектр дискретный.

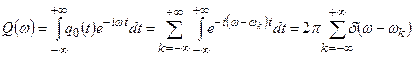(31)

Таким образом, свёртка (30)

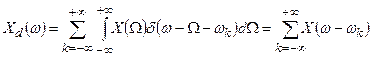(32)

Из выражения (32) следует, что спектр дискретного сигнала представляет собой периодически повторяющуюся функцию .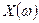

Сам факт того, что в результате дискретизации в спектре сигнала происходят качественные изменения, говорит о том, что исходный сигнал может быть искажён, так как он полностью определяется своим спектром. Однако с другой стороны периодическое повторение одного и того же спектра само по себе не вносит ничего нового в спектр, поэтому при определённых условиях, зная значения сигнала в отдельные моменты времени, можно найти какое значение этот сигнал принимал в любой другой момент времени, то есть получить исходный непрерывный сигнал. В этом состоит смысл теоремы Котельникова, которая накладывает условие на выбор частоты квантования в соответствии с максимальной частотой в спектре сигнала.

Теорема Котельникова: чтобы непрерывный сигнал можно было восстановить по его дискретным отсчётам, необходимо, чтобы частота квантования была выбрана больше удвоенной максимальной частоты в спектре сигнала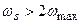

Если это условие нарушено, то после оцифровки сигнала произойдёт наложение периодически повторяющегося спектра (рис. 2). Получившийся в результате наложения спектр будет соответствовать другому сигналу.

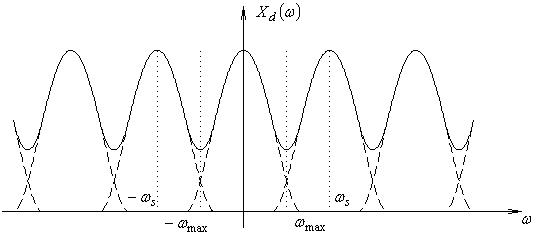
Рис. 2. Перекрывание спектров.