Свойства преобразования Фурье

Рассмотрим основные свойства преобразования Фурье.

Линейность. Рассмотрим функци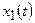и и 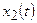, имеющие спектры 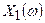и :

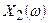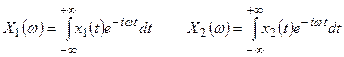(12)

Тогда спектр их линейной комбинации будет:

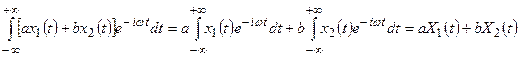(13)

Задержка во времени. Считаем, что известен спектр 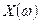сигнала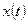

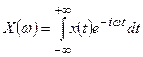(14)

Рассчитаем спектр сигнала, сдвинутого во времени: 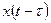. Обозначим аргумент функции новой переменной 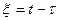, тогда 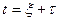и

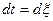
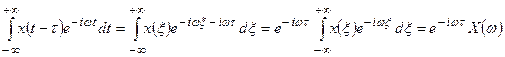(15)

Получили, что задержка сигнала на время 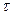приводит к умножению спектра на .

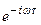Изменение масштаба. Считаем, что известен спектр 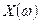сигнала 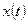, как через 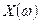выражается спектр сигнала 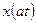. Вводим новую переменную 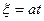, делаем замену переменной интегрирования .

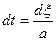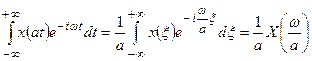(16)

Умножение на 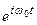. Как и в предыдущем случае, считаем, что известен спектр 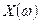сигнала 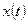. Найдем спектр этого сигнала, умноженного на .

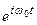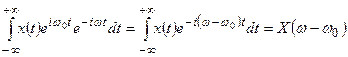(17)

Таким образом, умножение сигнала на 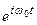приводит к смещению спектра на .

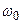Спектр производной. В данном случае ключевым моментом является абсолютная интегрируемость функции. Из того, что интеграл от модуля функции должен быть ограничен, следует, что на бесконечности функция должна стремиться к нулю. Интеграл от производной функции берётся по частям, получившиеся внеинтегральные слагаемые равны нулю, так как на бесконечности функция стремится к нулю.

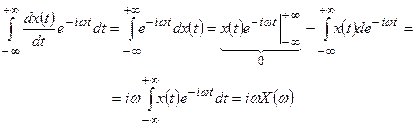(18)

Спектр интеграла. Найдем спектр сигнала 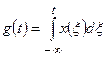. Причём будем считать, что 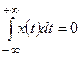, то есть у сигнала отсутствует постоянная составляющая. Это требование необходимо, чтобы внеинтегральные слагаемые были равны нулю, когда интеграл берётся по частям.

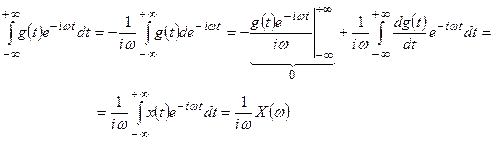(19)

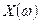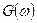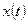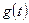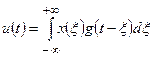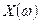Теорема о свёртке. Известно, что и спектры функций и соответственно. Требуется выразить спектр свертки через и 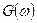. Для этого в интеграле Фурье от свёртки у одной из функций выполним замену переменой 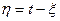, тогда в показателе экспоненты можно сделать замену 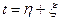. В результате такой замены двукратный интеграл будет равен произведению двух интегралов Фурье.

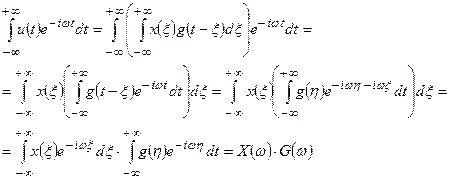(20)

Преобразование Фурье свёртки двух сигналов даёт произведение спектров этих сигналов.

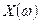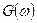Произведение сигналов. Известно, что и – спектры функци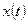й и 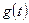соответственно. Требуется выразить спектр произведения 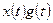через спектры 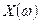и 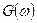. Подставим в интеграл Фурье вместо одного из сигналов, например 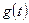, его выражение через обратное преобразование Фурье, а потом поменяем порядок интегрирования.

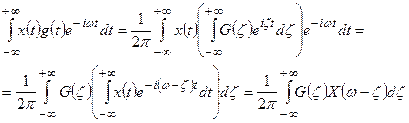(21)

Спектр произведения сигналов есть свёртка спектров этих сигналов.