Разностью двух множеств А и В называют такое множество 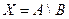 , в которое входят все элементы из А, не принадлежащие множеству В. При этом не предполагается, что множество В является частью множества А. Таким образом, при вычитании множества В из множества А из А удаляются пересечение А и В:
, в которое входят все элементы из А, не принадлежащие множеству В. При этом не предполагается, что множество В является частью множества А. Таким образом, при вычитании множества В из множества А из А удаляются пересечение А и В:
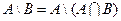 .
.
Например, если А – множество точек первого круга на рисунке 16, а В – множество точек второго круга, то и разностью является множество точек заштрихованной серповидной фигуры. При этом точки дуги MN удаляются из фигуры.
В случае, когда В – часть множества А, 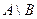 называют дополнением к В в множестве А и обозначают
называют дополнением к В в множестве А и обозначают 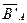 (разумеется, одно и то же множество В может иметь разные дополнения в разных содержащих его множествах А) (рис. 17). Например, дополнением множества четных чисел в множестве всех целых чисел является множество нечетных чисел. Дополнением множества всех квадратов в множестве прямоугольников является множество всех прямоугольников с неравными сторонами. А дополнением того же множества квадратов в множестве всех ромбов является множество ромбов с неравными смежными углами.
(разумеется, одно и то же множество В может иметь разные дополнения в разных содержащих его множествах А) (рис. 17). Например, дополнением множества четных чисел в множестве всех целых чисел является множество нечетных чисел. Дополнением множества всех квадратов в множестве прямоугольников является множество всех прямоугольников с неравными сторонами. А дополнением того же множества квадратов в множестве всех ромбов является множество ромбов с неравными смежными углами.
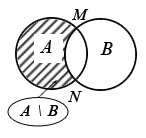
Рис. 16
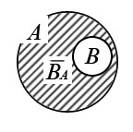
Рис. 17
 2015-06-28
2015-06-28 492
492








