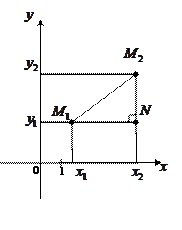2015-06-28
1372
Дано: 
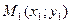и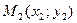 
.
Найти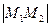 
.
Рассмотрим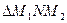 
. По теореме Пифагора:
;
;
; 
;
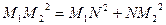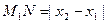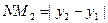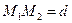
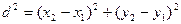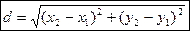
3.3. Уравнение линии. Уравнение прямой
с угловым коэффициентом
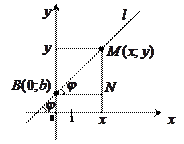Определение: уравнением линии на плоскости в прямоугольной системе координат 
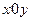называется уравнение 
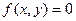, которому удовлетворяют координаты каждой точки данной линии и не удовлетворяют координаты любой точки плоскости, не лежащей на этой линии.
Замечание: геометрическим образом заданного уравнения не всегда является линия:
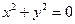– точка 
; 
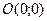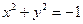– нет такой точки.
3.4. Уравнение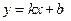 
– уравнение прямой
с угловым коэффициентом k
Дана прямая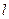 
, которая пересекает оси координат и не параллельна ни одной из них. Пусть угол наклона к положительному направлению оси Ox равен 
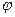. Угол 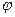отсчитывается от Ox против часовой стрелки 
(
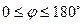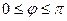) – угол наклона прямой 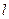к положительному направлению оси Ox. Точка пересечения с Oy – 
.
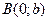Пусть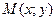 
– произвольная точка 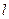. Рассмотрим 
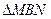. Он прямоугольный и имеет острый угол ; 
; 
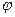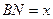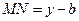. Найдем 
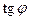(отношение противолежащего катета к прилежащему). 
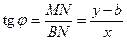. Обозначим 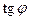через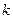 
. Имеем: 
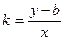или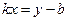 
, 
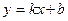– уравнение прямой с угловым коэффициентом .
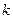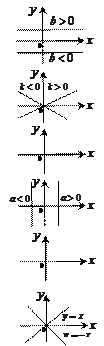Частные случаи:
1) 
, 
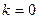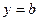– уравнение прямой, параллельной оси Ох и отстоящей от нее на 
;
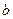2) 
, 
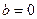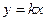– прямая проходит через начало координат;
3) 
, 
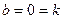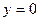– уравнение оси Ox;
4) 
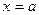– уравнение прямой, параллельной оси Oy и отстоящей от нее на 
;
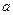5) 
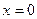– уравнение оси Oy;
6) 
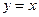– уравнение биссектрисы I и III координатных углов;
7) 
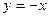– уравнение биссектрисы II и IV координатных углов.
