Любую прямую на плоскости можно задать уравнением: 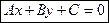 , где
, где 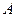 ,
, 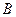 и
и 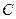 – коэффициенты, одновременно не равные нулю.
– коэффициенты, одновременно не равные нулю.
Справедливо утверждение: каждая прямая на плоскости с прямоугольной системой координат определяется уравнением первой степени, и, наоборот, каждое уравнение первой степени определяет некоторую прямую на плоскости.
Рассмотрим каждое из условий:
1) Пусть дана прямая 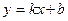 , в которой
, в которой 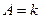 ,
, 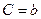 ,
, 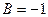 (
(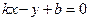 ). Если
). Если 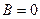 ,
, 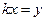 – тоже прямая. Итак, любая прямая – уравнение первой степени.
– тоже прямая. Итак, любая прямая – уравнение первой степени.
2) Покажем, что произвольному уравнению первой степени (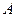 ,
, 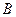 и
и 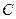 одновременно не равны 0) соответствует прямая на плоскости.
одновременно не равны 0) соответствует прямая на плоскости.
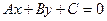 если
если 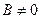 , то
, то 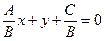 ,
, 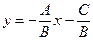 , где
, где 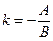 ,
, 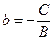 . Значит
. Значит 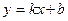 – прямая линия. Если
– прямая линия. Если 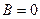 ,
, 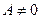 , то
, то 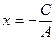 – уравнение прямой, параллельной оси Oy. Уравнение
– уравнение прямой, параллельной оси Oy. Уравнение 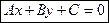 – общее уравнение прямой.
– общее уравнение прямой.
 2015-06-28
2015-06-28 406
406








